Hue Engine: Reversing the PWM functions
Introduction
This is the third post in the Reversing Philips Hue light driver series.
In the second part, I dumped the PWM data for various brightness / color temperature settings.
Problem statement
There are three functions of two parameters (color temperature, brightness) that define the PWM output channels:
I want to get a mathematical description of the generating function. Ideally exact, but a decently close approximation is fine, too.
The journey
Originally I had no idea where to even begin. I asked ChatGPT for advice as to
how to reverse engineer the two-parameter function. The answer I got was around
sklearn.preprocessing.LinearRegression.
That did not get me anywhere close to fitting the data. I fiddled around
with other python packages, namely scipy.optimize.curve_fit before giving
up, and asking for help on scicomp.
I was pointed at higher-order functions, spline approximation, and symbolic regression.
I tried them all, and mostly failed.
Then I briefly chatted with one of my colleagues (Balazs), who was immensely interested in the point of saturation.
See, the picture above was actually a lie. Actual data looked more like this:
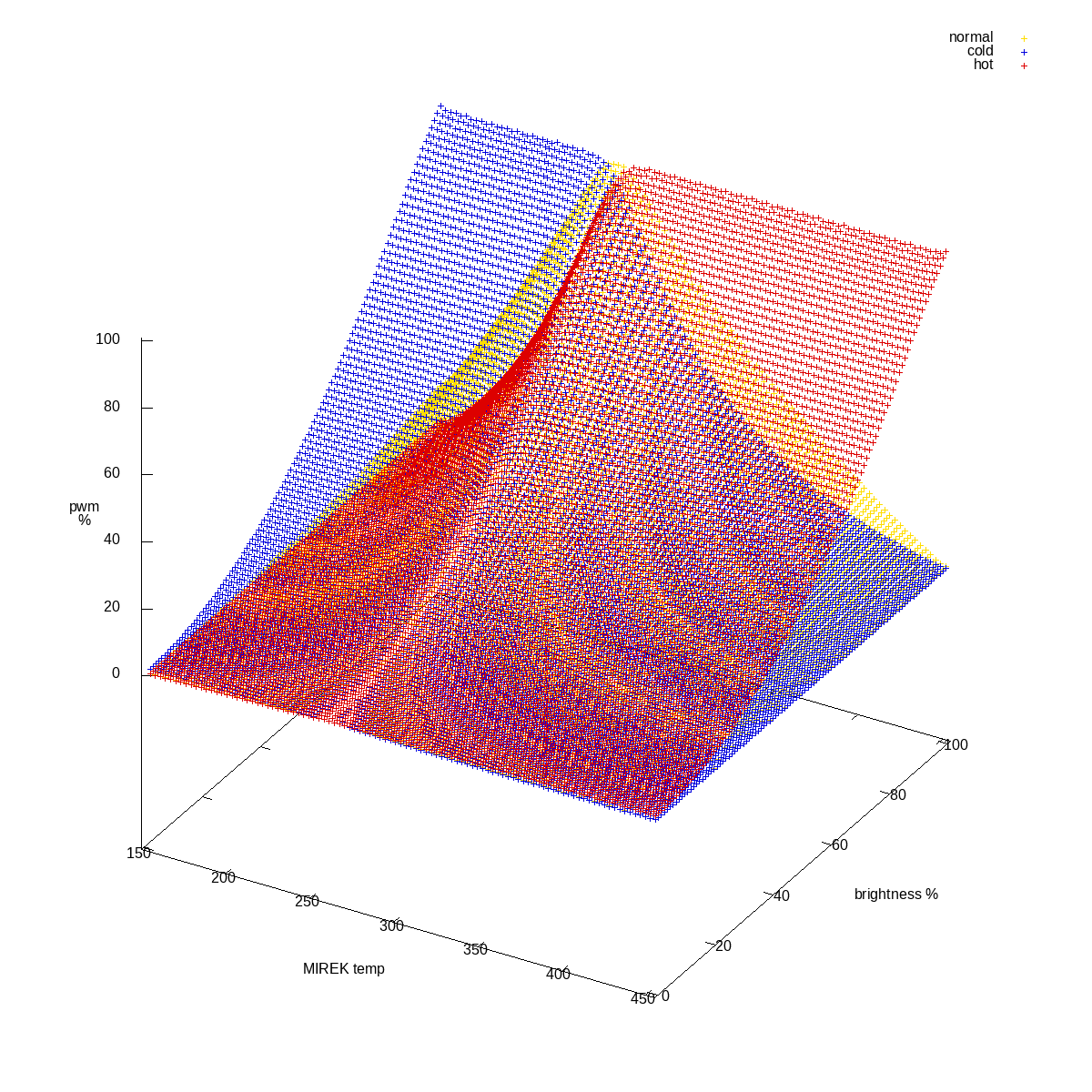 All three channels combined, original sparse data
All three channels combined, original sparse data
So I played a bit of a trick on myself by running the data through gnuplot with interpolation.
Balazs mentioned that there’s probably a sharp transition around the saturation, and that I should explore that further. Plus, that “everything around light is logarithmic”.
I decided to dense up the data, that’s the reason for the weird combos in
pwm-dumper.rb:
combos = []
mireks = (153.step(454, 5) + [454]).to_a
brightnesses = 0.step(100, 5).to_a
# Basic cartesian for 5-point matrix
combos += mireks.product(brightnesses)
# points around saturation
combos += (245..268).to_a.product(brightnesses)
# lower brightness
combos += mireks.product((0..15).to_a)
# every mirek at 90,95,100 brightness
combos += (153..454).to_a.product([90, 95, 100])
# every mirek at 90..100 brightness (step 2)
combos += (153..454).to_a.product(90.step(100, 2).to_a)
# DRY
combos.sort!.uniq!
Because I wanted to collect more data.
With that the shape is somewhat different:
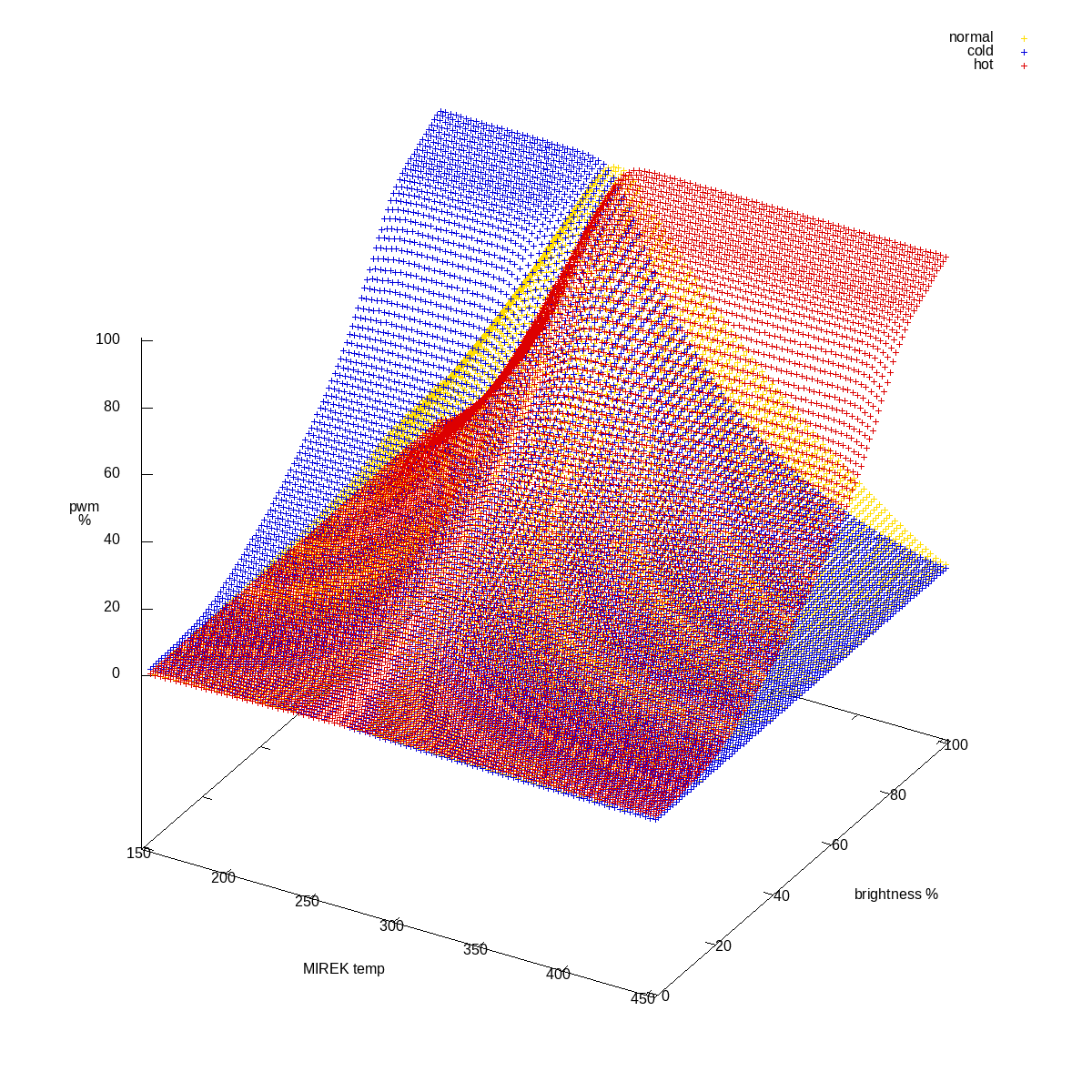 All three channels combined, final data
All three channels combined, final data
In order to get somewhere, I decided to project to 2d, to better see the curves:
Which was strangely symmetrical1. That got me thinking that I could maybe approximate brightness separately from the color-temperature.
So I took brightness at specific color temperature points (258 for normal,
223 for cold, 303 for hot), dumped it to json, and tried running linear
regression on that:
#!/usr/bin/env python3
import numpy as np
from scipy.optimize import curve_fit
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import json
with open('pwm-table-brightness.json', 'r') as file:
data = json.load(file)
brightness = np.array(data["brightness"])
normal = np.array(data["normal"])
cold = np.array(data["cold"])
hot = np.array(data["hot"])
def f(X, a, b, c):
x = X
return (a + b*x + c*x**2)
out = dict()
def pretty_print(name, popt, pcov, x_data, y_data):
print(name + ":")
print('popt:', popt)
print('pcov:', pcov)
perr = np.sqrt(np.diag(pcov))
print('perr:', perr)
y_pred = f((x_data), *popt)
mse = np.mean((y_data - y_pred)**2)
print("mse:", mse)
print()
popt, pcov = curve_fit(f, (brightness), normal)
out['normal'] = list(popt)
pretty_print('normal', popt, pcov, (brightness), normal)
popt, pcov = curve_fit(f, (brightness), cold)
out['cold'] = list(popt)
pretty_print('cold', popt, pcov, (brightness), cold)
popt, pcov = curve_fit(f, (brightness), hot)
out['hot'] = list(popt)
pretty_print('hot', popt, pcov, (brightness), hot)
with open('brightness-curves.json', 'w') as out_file:
json.dump(out, out_file, indent=4)
And it worked!
$ ./fit-brightness.py
normal:
popt: [ 9.99462593e-01 -3.40382133e-04 9.90325710e-03]
pcov: [[ 1.03065521e-05 -4.85098868e-07 4.14057014e-09]
[-4.85098868e-07 3.92993010e-08 -3.84299001e-10]
[ 4.14057014e-09 -3.84299001e-10 3.96309146e-12]]
perr: [3.21038193e-03 1.98240513e-04 1.99075148e-06]
mse: 8.65420496797531e-05
cold:
popt: [ 1.00003168e+00 -6.77564568e-05 9.90060890e-03]
pcov: [[ 8.83310608e-06 -4.15743520e-07 3.54855845e-09]
[-4.15743520e-07 3.36806564e-08 -3.29354462e-10]
[ 3.54855845e-09 -3.29354462e-10 3.39646949e-12]]
perr: [2.97205419e-03 1.83522904e-04 1.84295130e-06]
mse: 7.4171072704184e-05
hot:
popt: [9.98913762e-01 3.69293940e-05 9.89944166e-03]
pcov: [[ 8.09243226e-06 -3.80831025e-07 3.25035489e-09]
[-3.80831025e-07 3.08507557e-08 -3.01674354e-10]
[ 3.25035489e-09 -3.01674354e-10 3.11100027e-12]]
perr: [2.84472007e-03 1.75643832e-04 1.76380279e-06]
mse: 6.795975687969396e-05
Graphing that was a thing of beauty2:
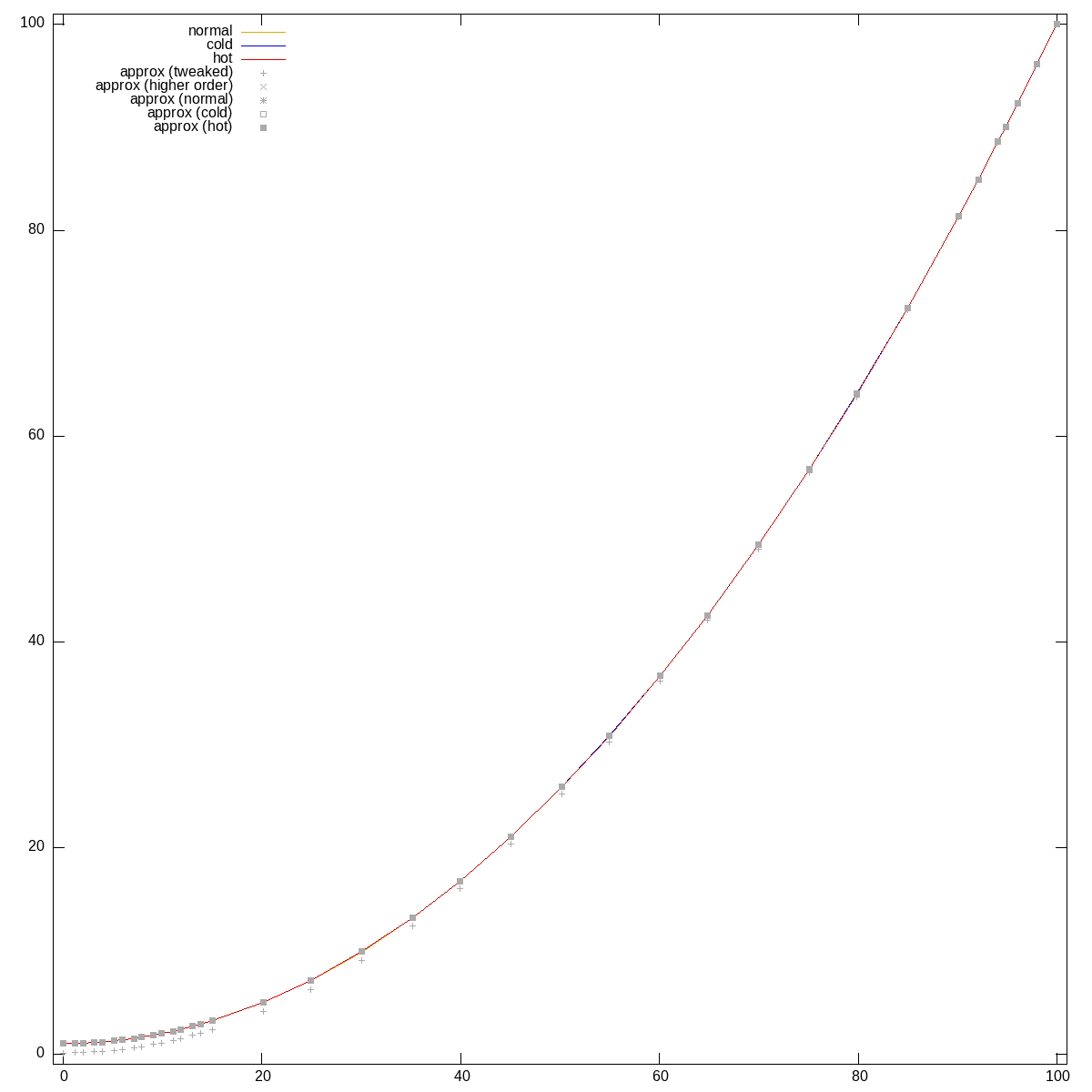 brightness approximation vs gathered data
brightness approximation vs gathered data
For all three channels the curve is virtually the same.
Half of the problem is solved!
I also retried the PySR (symbolic regression) on the brightness alone, and the solutions it came up with were interesting:
#PySR attempts at figuring out the brightness:
x0, x1 = mirek, brightness
# Try 1:
(Math.exp(Math.sin(Math.log(x0 ** -4.2384))) + -0.2912) *
((0.0038482 * (x1 * x1)) + 0.40689)
# Try 2:
((x1 * 0.003885924) *
(x1 * (Math.exp(Math.sin(Math.log(x0 ** -4.238486))) + -0.28776997))) +
Math.sin(x0 ** 0.58981854)
# Three:
((Math.sin(((2392.413 / x0) - 2.2254682) / 1.5551411) + -1.1892307) *
((x1 / -2.2668383) - -5.230437)) +
(x0 ** -0.32174507)
# Four:
((Math.cos(x0 / ((x0 + 8.137459) ** 0.548065)) - -1.2045676) *
(x1 * (x1 - -10.18817))) /
(x0 + -1.2525864)
Neither of them fits any better, btw. It’s hard to beat the parabola.
Figuring out the color-temperature curves
For the second half, I basically dumped the curves corresponding to 100% brightness to a json (again).
But this time I only chose the non-saturating parts – heeding Balazs’ advice about cutting off saturation.
Plus, I cut the normal curve in half – each slope separately.
The fit-pwmcurve.py script is almost the same, only uses higher
order polynomial:
#!/usr/bin/env python3
import numpy as np
from scipy.optimize import curve_fit
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import json
with open('pwm-table-fullbright.json', 'r') as file:
data = json.load(file)
mirek_n1 = np.array(data["mirek_n1"])
mirek_n2 = np.array(data["mirek_n2"])
mirek_c = np.array(data["mirek_c"])
mirek_h = np.array(data["mirek_h"])
normal1 = np.array(data["normal1"])
normal2 = np.array(data["normal2"])
cold = np.array(data["cold"])
hot = np.array(data["hot"])
def f(X, a, b, c, d, e, f):
#def f(X, a, b, c):
x = X
#return (a + b*x + c*x**2)
return (a + b*x + c*x**2 + d*x**3 + e*x**4 + f*x**5)
out = dict()
def pretty_print(name, popt, pcov, x_data, y_data):
print(name + ":")
print('popt:', popt)
print('pcov:', pcov)
perr = np.sqrt(np.diag(pcov))
print('perr:', perr)
y_pred = f((x_data), *popt)
mse = np.mean((y_data - y_pred)**2)
print("mse:", mse)
print()
popt, pcov = curve_fit(f, (mirek_n1), normal1)
out['normal1'] = list(popt)
pretty_print("normal1", popt, pcov, (mirek_n1), normal1)
popt, pcov = curve_fit(f, (mirek_n2), normal2)
out['normal2'] = list(popt)
pretty_print("normal2", popt, pcov, (mirek_n2), normal2)
popt, pcov = curve_fit(f, (mirek_c), cold)
out['cold'] = list(popt)
pretty_print("cold", popt, pcov, (mirek_c), cold)
popt, pcov = curve_fit(f, (mirek_h), hot)
out['hot'] = list(popt)
pretty_print("hot", popt, pcov, (mirek_h), hot)
with open('pwm-curves.json', 'w') as out_file:
json.dump(out, out_file, indent=4)
And again, more or less success!
$ ./fit-pwmcurve.py
normal1:
popt: [-6.64576279e+02 1.54463883e+01 -1.53120763e-01 7.87165097e-04
-1.99199066e-06 1.99958433e-09]
pcov: [[ 2.08112820e+06 -5.26665821e+04 5.29355676e+02 -2.64169984e+00
6.54631067e-03 -6.44532249e-06]
[-5.26665821e+04 1.33370507e+03 -1.34140119e+01 6.69849733e-02
-1.66099443e-04 1.63639238e-07]
[ 5.29355676e+02 -1.34140119e+01 1.35002861e-01 -6.74596769e-04
1.67383733e-06 -1.65008005e-09]
[-2.64169984e+00 6.69849733e-02 -6.74596769e-04 3.37307620e-06
-8.37475624e-09 8.26106428e-12]
[ 6.54631067e-03 -1.66099443e-04 1.67383733e-06 -8.37475624e-09
2.08061843e-11 -2.05364940e-14]
[-6.44532249e-06 1.63639238e-07 -1.65008005e-09 8.26106428e-12
-2.05364940e-14 2.02827454e-17]]
perr: [1.44261159e+03 3.65199270e+01 3.67427354e-01 1.83659364e-03
4.56137965e-06 4.50363691e-09]
mse: 0.27130540598011904
normal2:
popt: [ 2.82060879e+02 1.97594522e+00 -2.75937315e-02 1.04037626e-04
-1.70830613e-07 1.05251876e-10]
pcov: [[ 2.85378756e+04 -4.07703744e+02 2.31089911e+00 -6.49665780e-03
9.06029906e-06 -5.01553042e-09]
[-4.07703744e+02 5.82909617e+00 -3.30649902e-02 9.30258061e-05
-1.29830043e-07 7.19217666e-11]
[ 2.31089911e+00 -3.30649902e-02 1.87700343e-04 -5.28476718e-07
7.38104026e-10 -4.09180744e-13]
[-6.49665780e-03 9.30258061e-05 -5.28476718e-07 1.48905170e-09
-2.08122909e-12 1.15459425e-15]
[ 9.06029906e-06 -1.29830043e-07 7.38104026e-10 -2.08122909e-12
2.91101687e-15 -1.61608217e-18]
[-5.01553042e-09 7.19217666e-11 -4.09180744e-13 1.15459425e-15
-1.61608217e-18 8.97814975e-22]]
perr: [1.68931571e+02 2.41435212e+00 1.37003775e-02 3.85882326e-05
5.39538402e-08 2.99635608e-11]
mse: 0.006974028051178422
cold:
popt: [-2.70308303e+03 4.98116995e+01 -3.23154212e-01 9.85997632e-04
-1.45136896e-06 8.34172592e-10]
pcov: [[ 5.06924244e+05 -7.39439590e+03 4.27063357e+01 -1.22095400e-01
1.72835522e-04 -9.69432519e-08]
[-7.39439590e+03 1.07964881e+02 -6.24148855e-01 1.78609082e-03
-2.53066689e-06 1.42070670e-09]
[ 4.27063357e+01 -6.24148855e-01 3.61166666e-03 -1.03450103e-05
1.46710519e-08 -8.24362266e-12]
[-1.22095400e-01 1.78609082e-03 -1.03450103e-05 2.96590996e-08
-4.21002537e-11 2.36770736e-14]
[ 1.72835522e-04 -2.53066689e-06 1.46710519e-08 -4.21002537e-11
5.98139094e-14 -3.36688140e-17]
[-9.69432519e-08 1.42070670e-09 -8.24362266e-12 2.36770736e-14
-3.36688140e-17 1.89683205e-20]]
perr: [7.11986126e+02 1.03906151e+01 6.00971436e-02 1.72218174e-04
2.44568823e-07 1.37725526e-10]
mse: 0.4012776209257108
hot:
popt: [ 8.79835997e+03 -2.26331852e+02 2.30636305e+00 -1.16593419e-02
2.92757451e-05 -2.91413229e-08]
pcov: [[ 1.09785188e+06 -2.70992296e+04 2.65148674e+02 -1.28561968e+00
3.08967716e-03 -2.94502444e-06]
[-2.70992296e+04 6.69484813e+02 -6.55602586e+00 3.18145015e-02
-7.65206663e-05 7.29957072e-08]
[ 2.65148674e+02 -6.55602586e+00 6.42549032e-02 -3.12069847e-04
7.51206580e-07 -7.17171085e-10]
[-1.28561968e+00 3.18145015e-02 -3.12069847e-04 1.51689381e-06
-3.65438912e-09 3.49158219e-12]
[ 3.08967716e-03 -7.65206663e-05 7.51206580e-07 -3.65438912e-09
8.81093356e-12 -8.42500606e-15]
[-2.94502444e-06 7.29957072e-08 -7.17171085e-10 3.49158219e-12
-8.42500606e-15 8.06220472e-18]]
perr: [1.04778427e+03 2.58744046e+01 2.53485509e-01 1.23162243e-03
2.96832167e-06 2.83940218e-09]
mse: 0.26053485003543214
There was a slight issue with the cold channel (and to a lesser
degree with the hot channel), which I worked around by injecting
fake data:
# Manual curve tuning using fake data (sigh)
data_fullbright['mirek_c'] << 450
data_fullbright['cold'] << 0.5
data_fullbright['mirek_c'] << 452
data_fullbright['cold'] << 0.5
data_fullbright['mirek_c'] << 454
data_fullbright['cold'] << 0.2
data_fullbright['mirek_c'] << 456
data_fullbright['cold'] << -0.3
data_fullbright['mirek_c'] << 458
data_fullbright['cold'] << -0.8
data_fullbright['mirek_h'] << 152
data_fullbright['hot'] << -1
But other than that, pretty nice fit:
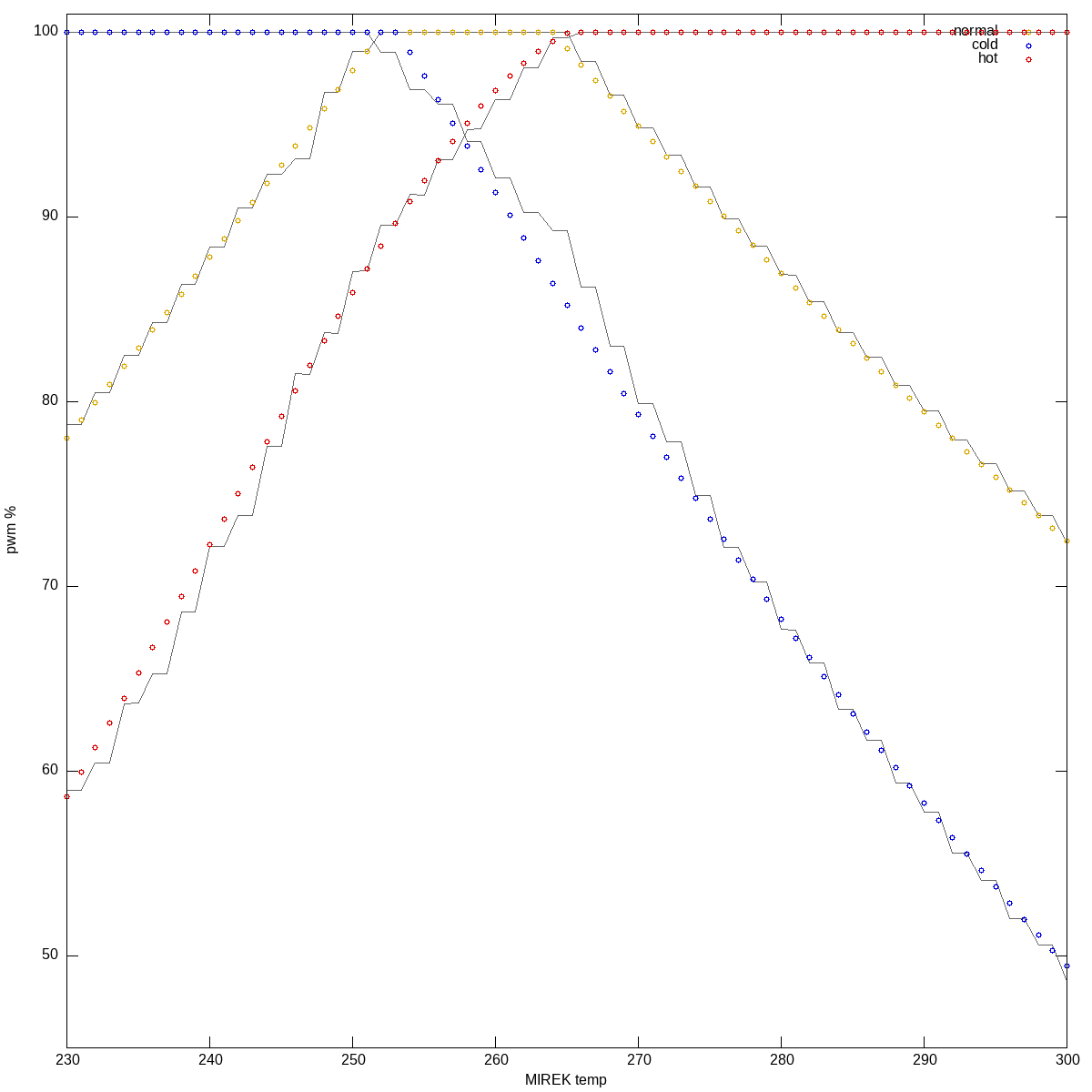 color temp curves, restricted to 230..300
color temp curves, restricted to 230..300
Putting it together
To put it together, I basically wrapped the two JSON output files in Ruby, and for the color temperature curve I stitched the individual parts together for the various intervals.
It ain’t pretty, but it works:
#!/usr/bin/env ruby
require 'json'
require 'pp'
# Correct brightness, optionally using one of the alt curve approximations
def correct_brightness(brightness, name = 'normal')
# ./fit-brightness.py -- for now.
$brightnesses ||= JSON.parse(File.read('brightness-curves.json'))
a, b, c = $brightnesses[name]
x = brightness
(a + b*x + c*x**2)
end
def _pwm_for(name, mirek)
# ./fit-pwmcurve.py -- for now.
$pwm_curves ||= JSON.parse(File.read('pwm-curves.json'))
curve = $pwm_curves[name]
x = mirek
a, b, c, d, e, f = *curve
out = (a + b*x + c*x**2 + d*x**3 + e*x**4 + f*x**5)
# clamp
if out > 100.0
100.0
elsif out < 0.0
0.0
else
out
end
end
# Approximate PWM value for channel name given mirek and brightness
def pwm_approximate(name, mirek, brightness)
pwm100 = if name == 'normal'
case mirek
when 153..252
_pwm_for('normal1', mirek)
when 265..454
_pwm_for('normal2', mirek)
else
100.0
end
elsif name == 'cold'
if mirek > 449
0.0
elsif (251..454).include?(mirek)
_pwm_for('cold', mirek)
else
100.0
end
elsif name == 'hot'
if mirek < 156
0.0
elsif (153..266).include?(mirek)
_pwm_for('hot', mirek)
else
100.0
end
else
0.0
end
(pwm100 * correct_brightness(brightness, name)/100.0)
end
I was obviously curious how well it stacks up. I evaluated the entire
space and drew delta of actual - approximated3:
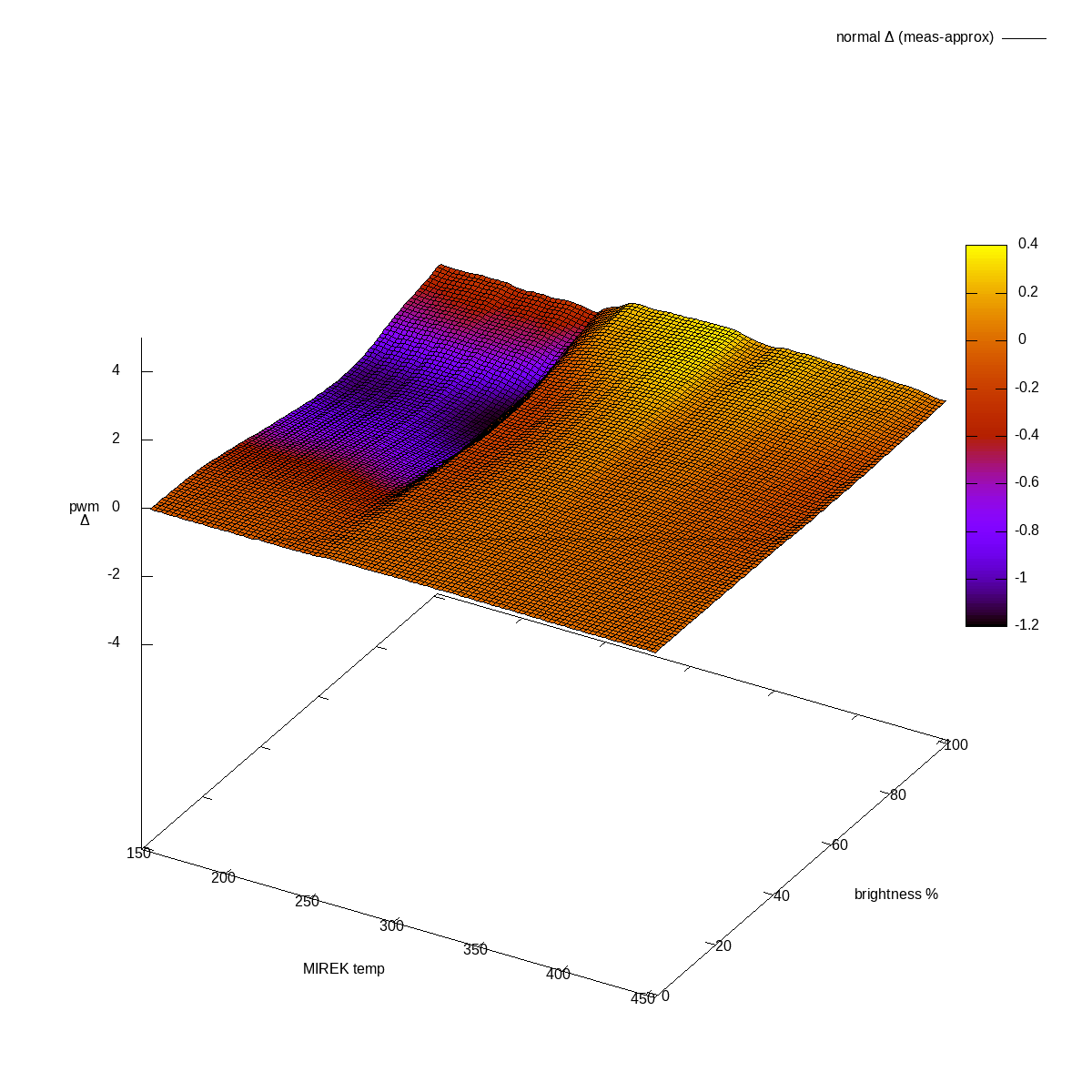 Normal channel, difference actual-approximated
Normal channel, difference actual-approximated
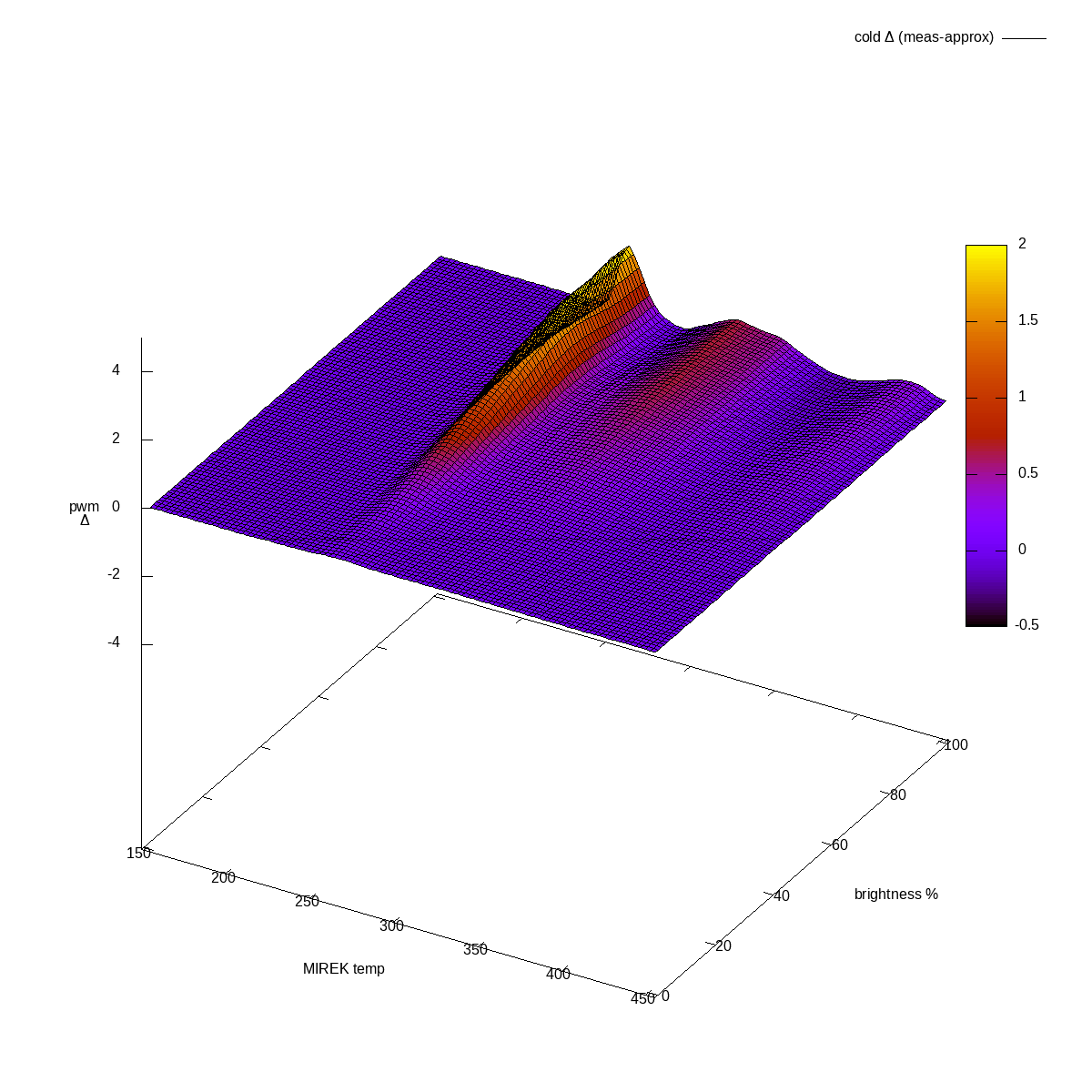 Cold channel, difference actual-approximated
Cold channel, difference actual-approximated
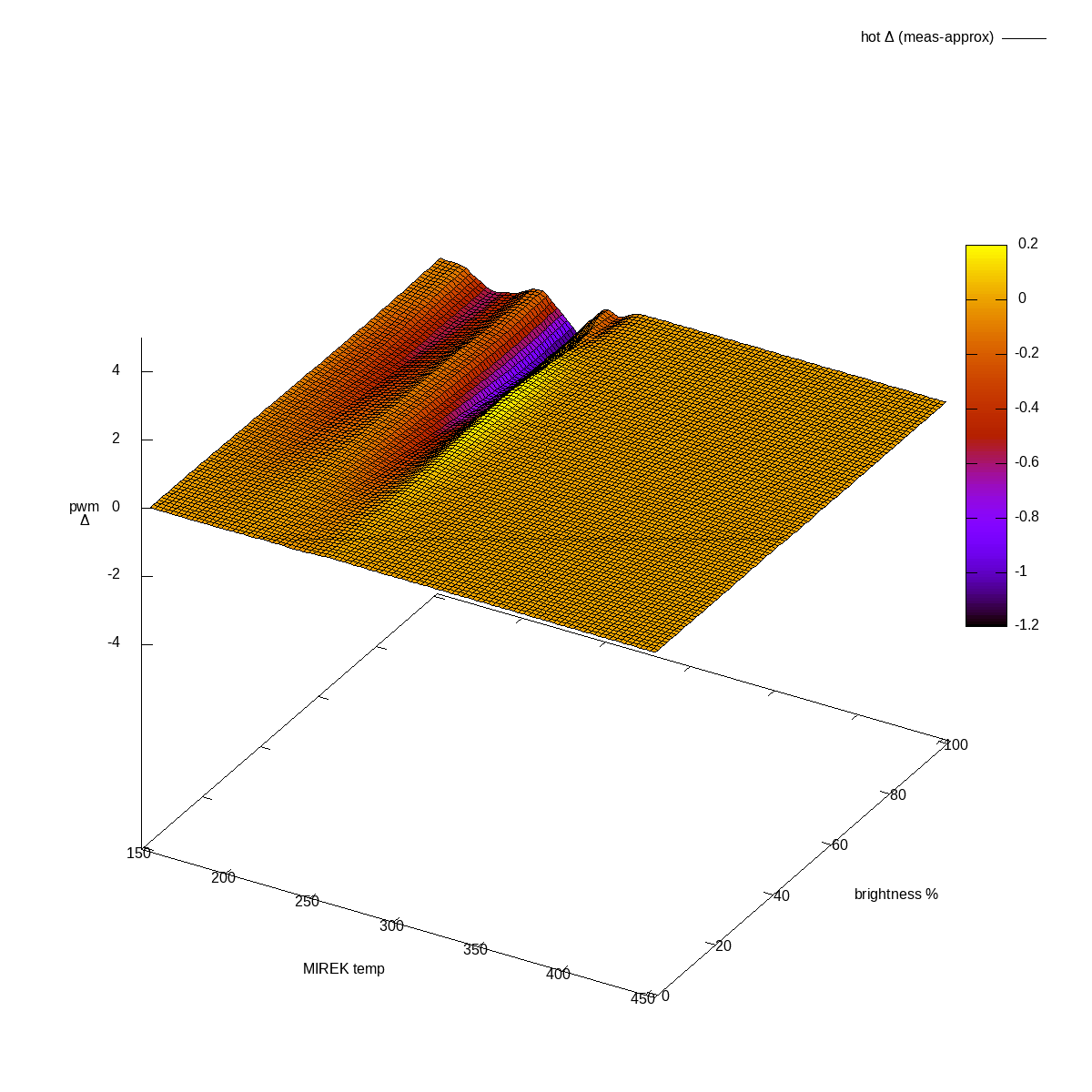 Hot channel, difference actual-approximated
Hot channel, difference actual-approximated
Plus the same in percents (diff divided by actual value):
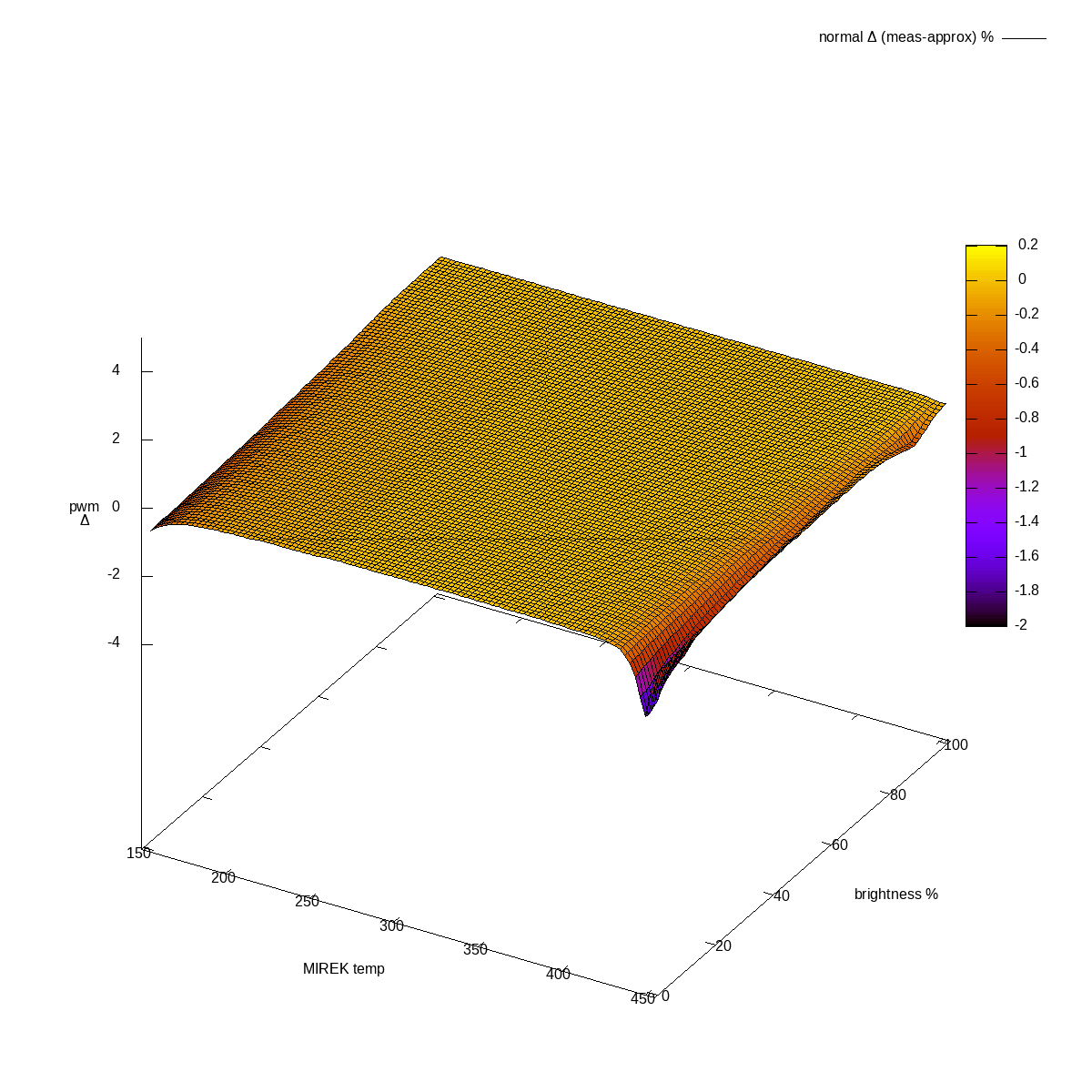 Normal channel, difference actual-approximated, in %
Normal channel, difference actual-approximated, in %
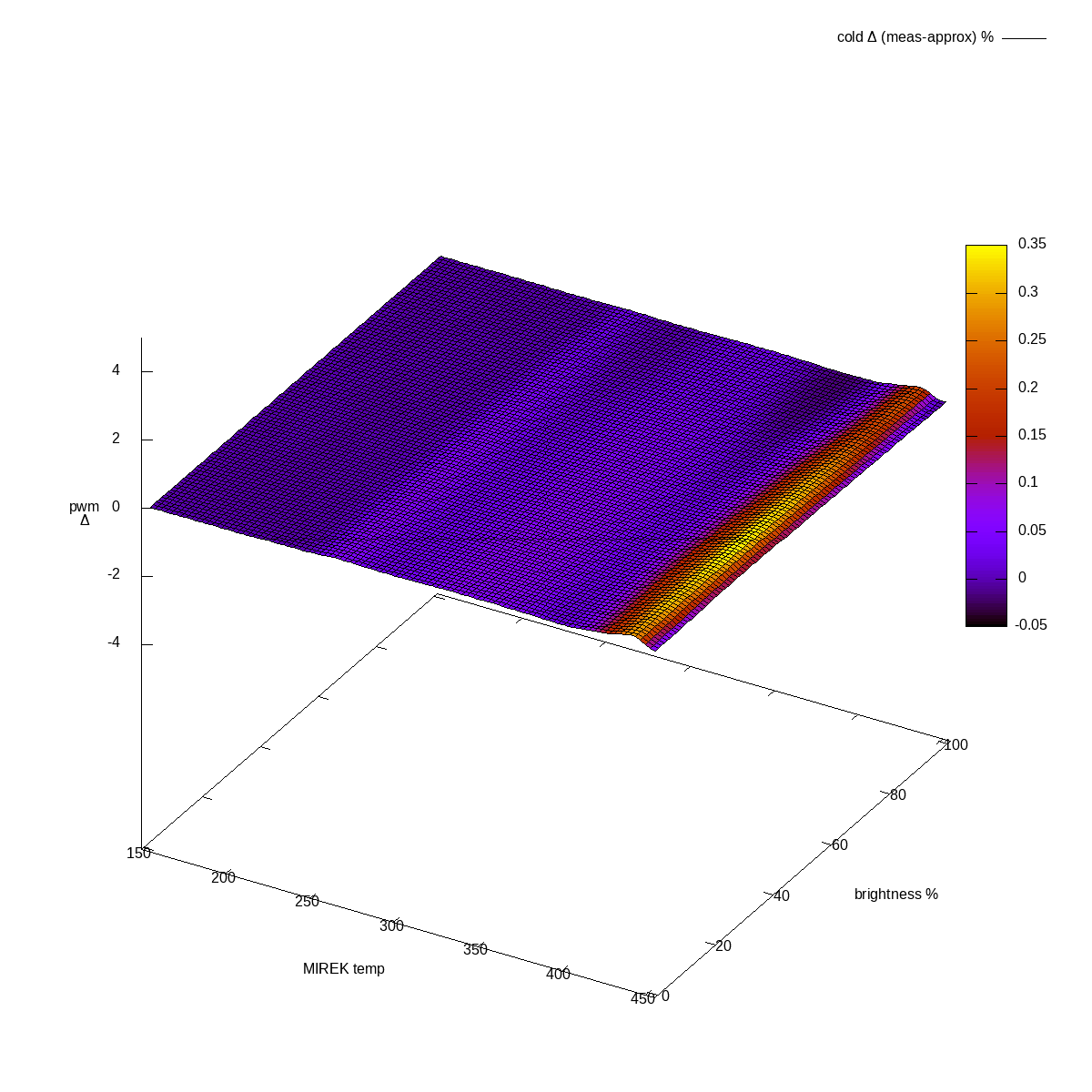 Cold channel, difference actual-approximated, in %
Cold channel, difference actual-approximated, in %
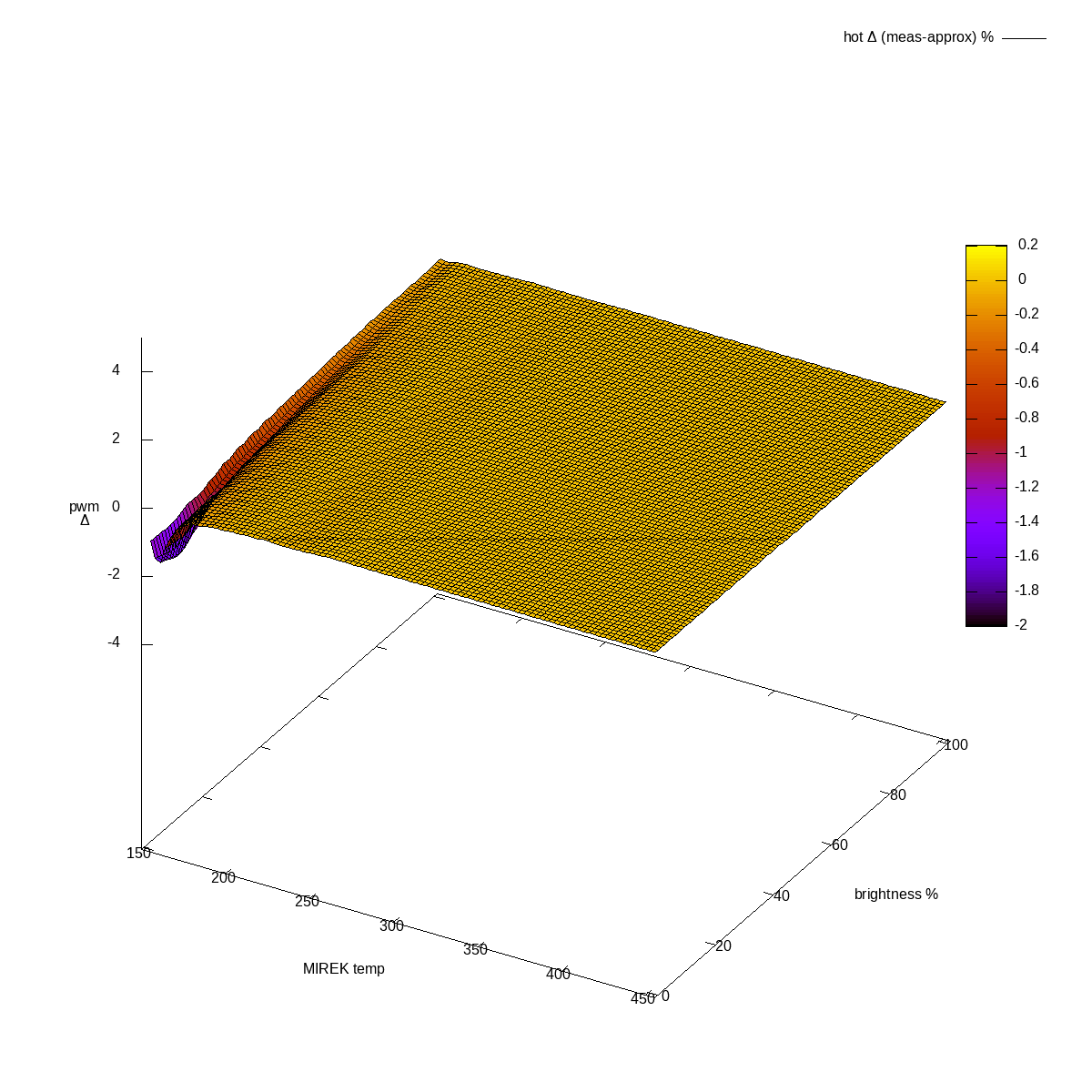 Hot channel, difference actual-approximated, in %
Hot channel, difference actual-approximated, in %
Closing words
Unless I messed up in some major way4, I now have the math description needed for driving the light.
Question remains whether I can efficiently calculate the
a + b*x + c*x**2 + d*x**3 + e*x**4 + f*x**5 on ESP32-C6.
If not, I can always revert to using tables.
In any case, breadboarding some prototype is going to be my next step.
Stay tuned.
-
Pay no attention to the
tweakedfunc, that was me manually trying to simplify to[0.1 -3.4e-04 10e-03]. Mostly works, but undershoots at lower brightness. ↩ -
Originally I just drew one plot over the other, but the difference was imperceptible. ↩
-
In the unlikely event that you want to check my homework (or simply want some of the code I wrote for this), ask. ↩
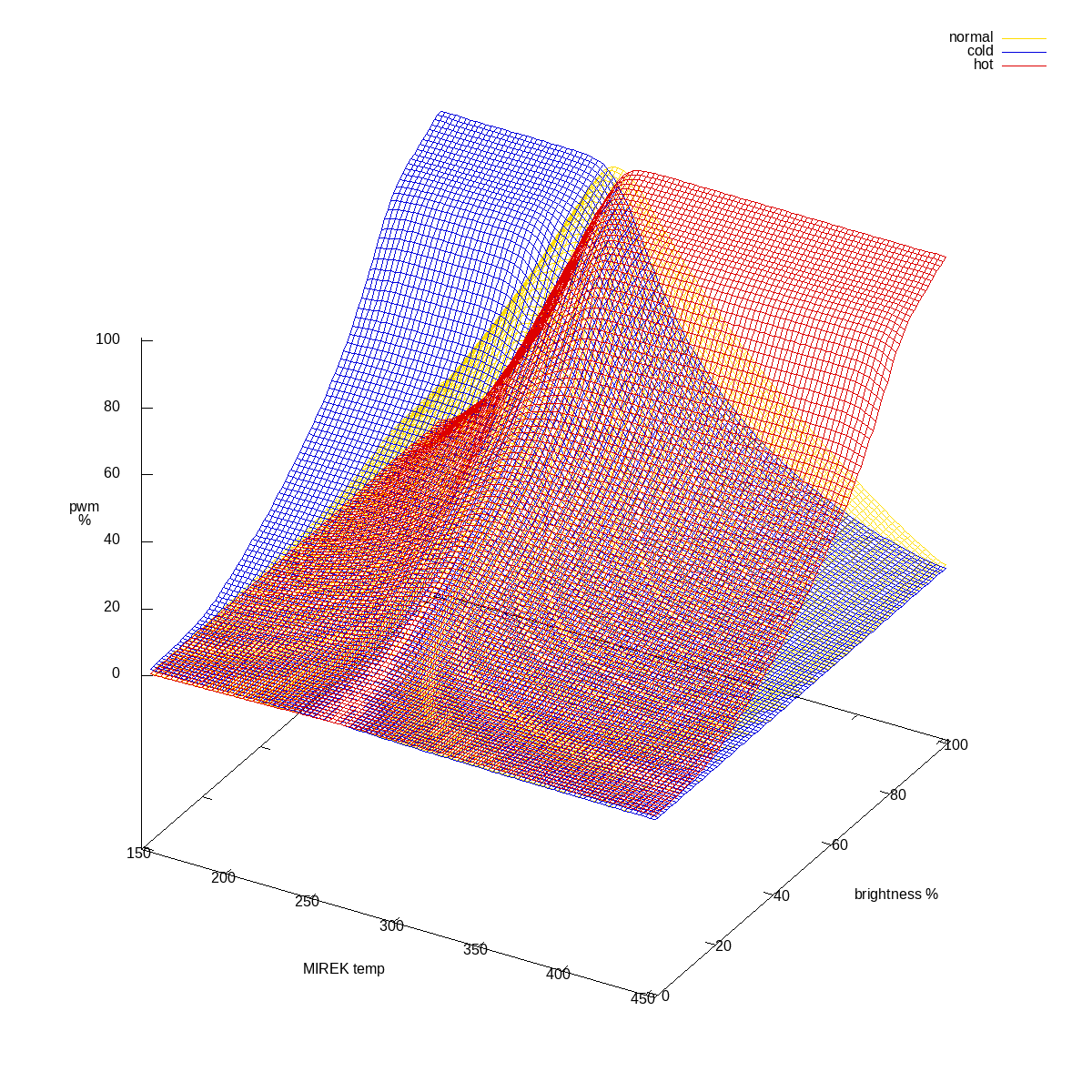 All three channels combined
All three channels combined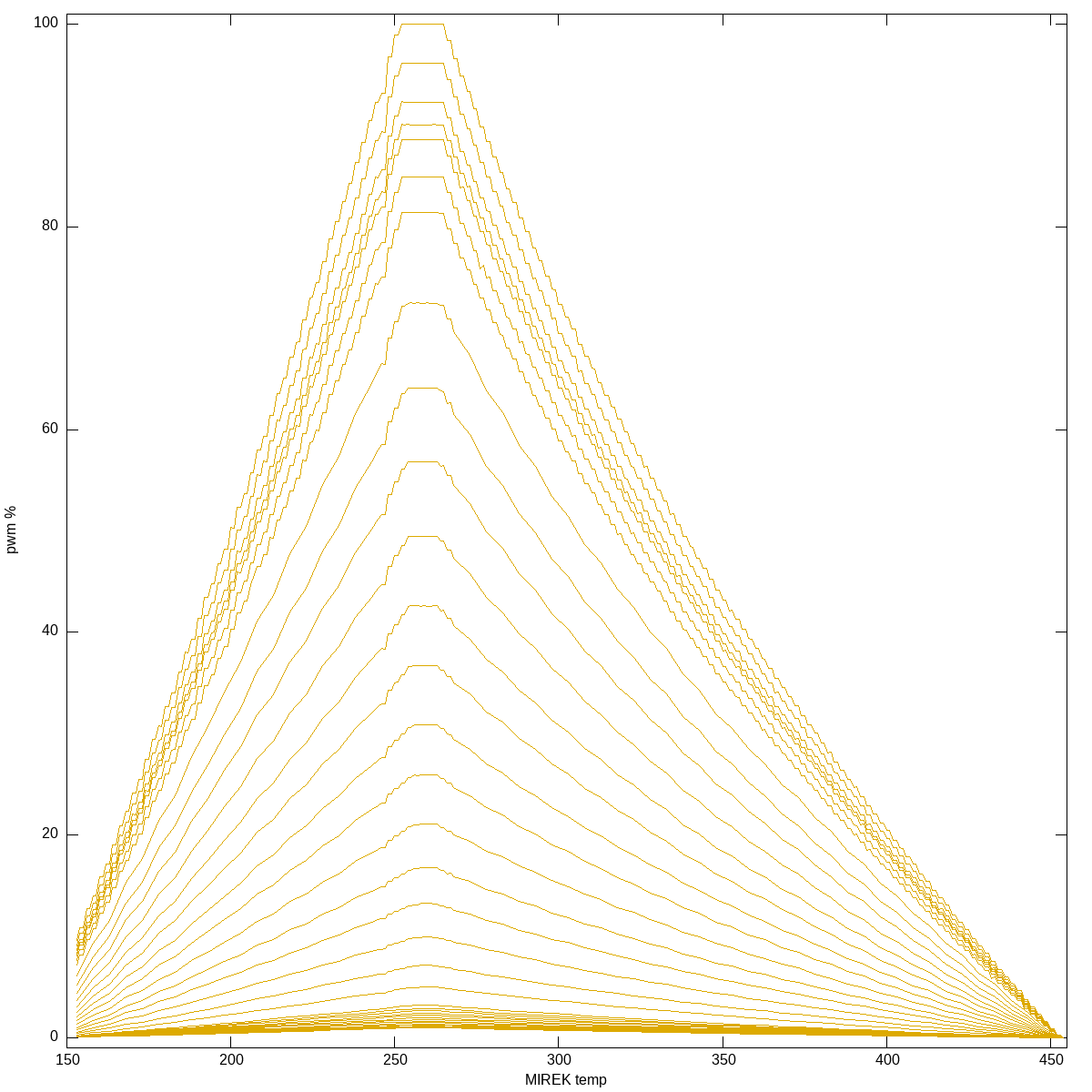 Normal channel, 2d plot
Normal channel, 2d plot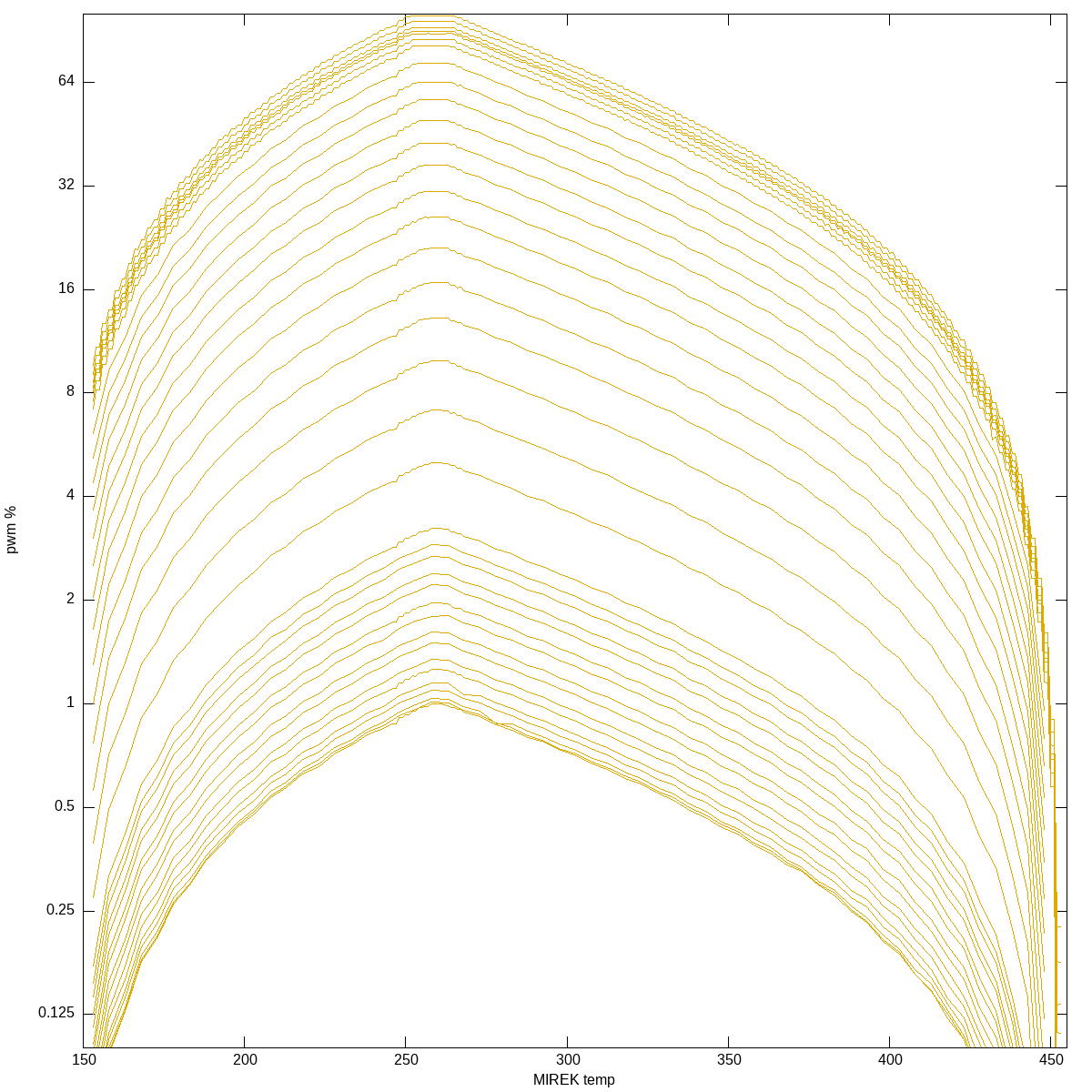 Normal channel, 2d log-plot
Normal channel, 2d log-plot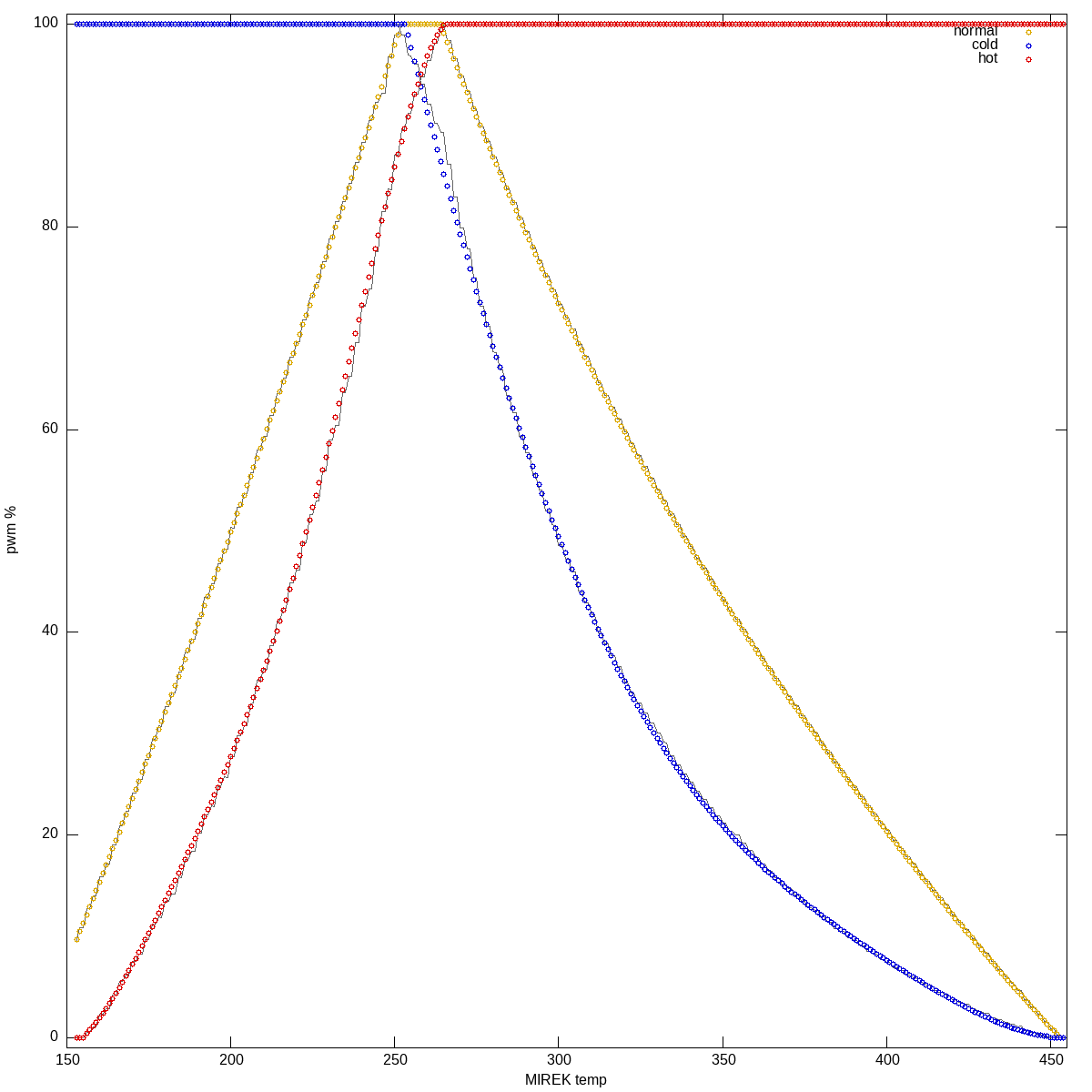 color temp curves, full
color temp curves, full