Engineering a better Anagrammer, part II

Introduction

In a previous post in the Anagrammer series I looked at the history of the Anagrammer project and vowed to take a stab at fixing the somewhat terrible tail latency:

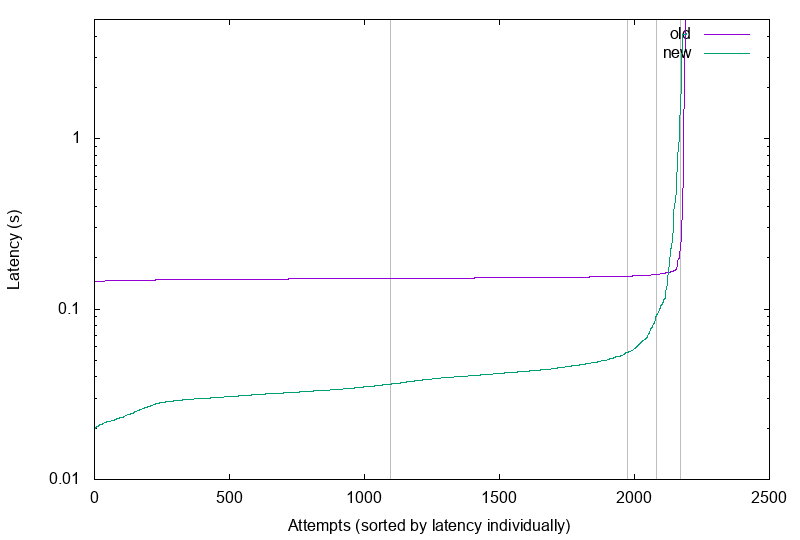click to enlarge; vertical lines mark 50th, 90th, 95th and 99th percentile.

This post will be a dive into the wonderful world of Ruby performance optimization, with a healthy side dish of fail (on my part).

More precisely, and with the benefit of hindsight… I’ll tackle the importance of:

1. Knowing what you’re getting yourself into
2. Knowing what you’re measuring
3. Knowing what you’re optimizing for
4. The tradeoff of performance vs. readability¹

And then I’ll discuss in depth the final result of many evenings worth of “fun”² as well as what changed to achieve that level of awesome.

Sounds good? Let’s dive in.

The importance of…

…knowing what you’re getting yourself into

When I set out to look at the tail latency, I thought to myself: it’ll be easy, barely an inconvenience. I’ll just analyze the outliers… profile the execution, maybe get rid of some object creation or some such.

Oh boy.

The trouble with the tail latency³ is – in hindsight – simple: If you give the algorithm well chosen input⁴, it is bound to be searching for a long time.

So while often a tail latency can be caused by an ineffective algorithm with bad big-O complexity, sometimes it can also be that the input problem is too big to solve.

Which is exactly the hell I run into.

By analyzing the poorly performing inputs from my test set⁵ revealed that often the dictionary trimming isn’t what one would hope for:

[:loading_cache, "data/czech.txt.msh"]
[:full_dict_size, 142801] # full dictionary: 142k buckets
[:trimmed_dict_ind_size, 7595]
[:trimmed_dict_total_size, 25684] # trimmed to 25k entries (in 7.5k buckets)
[:hints, [["d", 2716], ["p", 3197], ["m", 3283], ["y", 3294], ["v", 3459],
  ["l", 3460], ["r", 3495], ["t", 3549], ["s", 3576], ["n", 3637],
  ["o", 3915], ["e", 4170], ["i", 4328], ["a", 4539]]]
  # but best hint is 2.7k entries, so at least 2716 * ~3k candidates? ouch.

while often you get much luckier:

[:loading_cache, "data/czech.txt.msh"]
[:full_dict_size, 142801]
[:trimmed_dict_ind_size, 1312]
[:trimmed_dict_total_size, 2943]
[:hints, [["b", 341], ["y", 443], ["c", 500], ["p", 538], ["u", 589],
  ["s", 604], ["e", 614], ["o", 619], ["r", 625], ["k", 652],
  ["i", 658], ["l", 665]]]
  # 341 * ~500 combos to check. yawn?

So the idea of fixing the tail latency once and for all… is by default nonsense. The best I can hope (barring a miracle insight) is to close the gap.

…knowing what you’re measuring

When I set out to benchmark in the previous post, I naively assumed that the simple impact of GC and the chosen webserver/framework will be negligible.

So when I started improving the code, I tested it on known outliers (inputs that took too long). And then to verify the behavior across the board, I started benchmarking the improvements with a similar script as previously:

#!/usr/bin/env ruby
require 'open-uri'
require 'pp'

def old_anagrammer(input, words)
	sz = 0
	a, b = nil
	Dir.chdir('./data') do
		a = Time.now
		u = "http://localhost:3000/anagram?input=#{input}" + 
			"&dict=czech&maxwords=#{words}"
		data = open(u).read.split(/\n/)
		pp [:new, input, words, data] if $DEBUG
		sz = data.size
		b = Time.now
	end
	[b - a, sz]
rescue Net::OpenTimeout
	STDERR.puts [:timeout_old, input, words].inspect
	retry
end

def new_anagrammer(input, words)
	sz = 0
	a, b = nil
	Dir.chdir('./data') do
		a = Time.now
		u = "http://localhost:3001/anagram?input=#{input}" + 
			"&dict=czech&maxwords=#{words}"
		data = open(u).read.split(/\n/)
		pp [:new, input, words, data] if $DEBUG
		sz = data.size
		b = Time.now
	end
	[b - a, sz]
rescue Net::OpenTimeout
	STDERR.puts [:timeout_new, input, words].inspect
	retry
end

inputs = File.read('presmy_noaccents').split(/\n/)
#inputs = ["amd duron"]
for input in inputs
	input_clean = input.chars.reject { |x| x !~ /[a-z]/ }.join
	o2 = old_anagrammer(input_clean, 2)
	o3 = old_anagrammer(input_clean, 3)
	n2 = new_anagrammer(input_clean, 2)
	n3 = new_anagrammer(input_clean, 3)
	puts [input.gsub(/,/, ''), o2, o3, n2, n3].flatten.map(&:to_s).join(',')
end

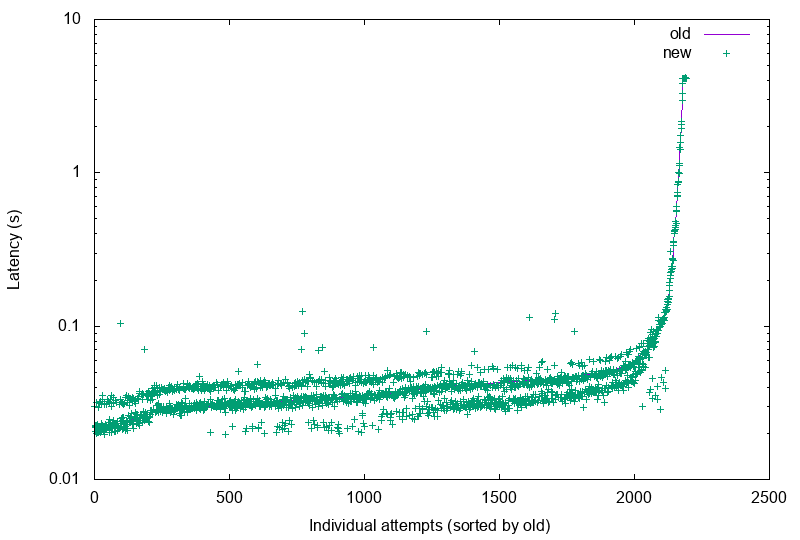
And in a moment of desperation⁶ it dawned on me that I might want to run the benchmark on the same code, to see the variance. I almost fell out of my chair when I saw this:

That’s a variability of up to ~100ms. Which diminishes the trust in the results, doesn’t it?

And while in an ideal world I’d go and write up a webserver-less version of the benchie script, I opted for this end-to-end variant, because in the end, the choice of language, webserver, and framework… factors into the end result.

Just maybe would be nice to figure this out beforehand and not when I was almost ready to throw in the towel.

…knowing what you’re optimizing for

I should probably say “remembering” instead of “knowing” here.

During the optimizations I’ve gotten into a situation where the result was significantly faster (25%+) than the baseline, but unfortunately ate 2x memory.

Which is a major bummer when you’re resource constrained⁷.

But I’ll get to this in a bit.

…the tradeoff of performance vs. readability

When I rewrote the anagrammer to use the Parallel arithmetics trick found in the gson.c, I went for the OOP way of writing it:

aa = ParallelArith.new(6, [0b10101, 0b01010, 0b10101])
bb = ParallelArith.new(6, [0b11, 0b11, 0b11])
p :vals
p aa    # => #<ParallelArith @bitsize=6, @max=63, @ar=[5, 2, 5, 2, 5, 0]>
p bb    # => #<ParallelArith @bitsize=6, @max=63, @ar=[7, 7, 0, 0, 0, 0]>
p aa-bb # => #<ParallelArith @bitsize=6, @max=63, @ar=[2, 7, 2, 0, 5, 0]>
p :indicators
p [aa.indicator, bb.indicator, (aa-bb).indicator].map { |x| "%06b" % x }
# => ["000111", "000111", "000111"]
p :vectors
p aa.vector      # => [21, 10, 21]
p bb.vector      # => [ 3,  3,  3]
p (aa-bb).vector # => [18,  7, 18]
p :lsb
p (aa-bb)[0]     # => 2
p :msb
p (aa-bb)[-1]    # => 0
p :==
p aa==bb         # => false
p aa.dup == aa   # => true
p ParallelArith.new(6, [0, 0, 0]) == ParallelArith.new(6, []) # => true
p :inv_i
p [aa.inverse_indicator, bb.inverse_indicator, (aa-bb).inverse_indicator].
  map { |x| "%06b" % x } # => ["..1000", "..1000", "..1000"]
p [aa.inverse_indicator(5), bb.inverse_indicator(5), (aa-bb).inverse_indicator(5)].
  map { |x| "%06b" % x } # => ["011000", "011000", "011000"]

which ends up with a reasonable interface… that turns out to be dog slow.

The root cause is the hidden object creation that constructs like the following lend themselves to:

class ParallelArith
  def initialize(bitsize, vector)
    # ...
  end

  def -(other)
    # ...
  end
end

That interface basically makes two performance killing mistakes:

1. Wraps low-level primitive (Array) into a higher-level class
2. Forces new object creation on every a-b call

If subtraction is the core of your algorithm, the last thing you want is to keep on creating composite classes.

So if you choose interface like:

class ParallelArith
  def initialize; raise "you do not instantiate me"; end

  def self.get(bitsize, vector)
    if vector
      # ...
    else
      Array.new(bitsize, 0)
    end
  end

  # for given bitsize `sz` compute `a` - `b` and store it in `o`, returning `carry`
  def self.sub2(sz, a, b, o)
    # ...
  end
end

you might get a double benefit.

First, the OOP crowd will run for the hills – because all of a sudden you’re in structured programming land.

But more importantly – you transform the implicit object creation on each subtraction into calls that say “do a minus b and stick the result in o”. And guess what? If you pre-allocate the o and re-use it many times over (e.g. in an iterator running through the dictionary), you don’t incur the penalty of constant memory allocation (and GC down the road).

Of course, the downside is that instead of easily understandable code that says a - b you get much less transparent calls like sub2(6, a, b, o). Not to mention that all of a sudden all of your arguments are just arrays of numbers. Have fun #inspect-ing your code.

I have a suspicion that one could retain some of the sanity of OOP (having the arrays wrapped in ParallelArith) with a different interface. If it weren’t for the vast difference in memory (and marshalled) footprint between the two versions:

# old
a = ParallelArith.new(6, [0b10101, 0b01010, 0b10101])
b = ParallelArith.new(6, [0b10101, 0b01010, 0b10101])
c = ParallelArith.new(6, [0b10101, 0b01010, 0b10101])
a # => #<ParallelArith @bitsize=6, @max=63, @ar=[5, 2, 5, 2, 5, 0]>
Marshal.dump(a).size # => 58
Marshal.dump([a, b, c]).size # => 116
ObjectSpace.memsize_of(a) + ObjectSpace.memsize_of(a.ar) # => 128
# and the memsize is incomplete, because we also hold 2 more Integers

# new
a = ParallelArith.get(6, [0b10101, 0b01010, 0b10101])
b = ParallelArith.get(6, [0b10101, 0b01010, 0b10101])
c = ParallelArith.get(6, [0b10101, 0b01010, 0b10101])
a # => [5, 2, 5, 2, 5, 0]
Marshal.dump(a).size # => 16
Marshal.dump([a, b, c]).size # => 46
ObjectSpace.memsize_of(a) # => 88

And if I’m to close the gap in terms of performance while also retaininig reasonable memory footprint, I have to go with the worse readability.

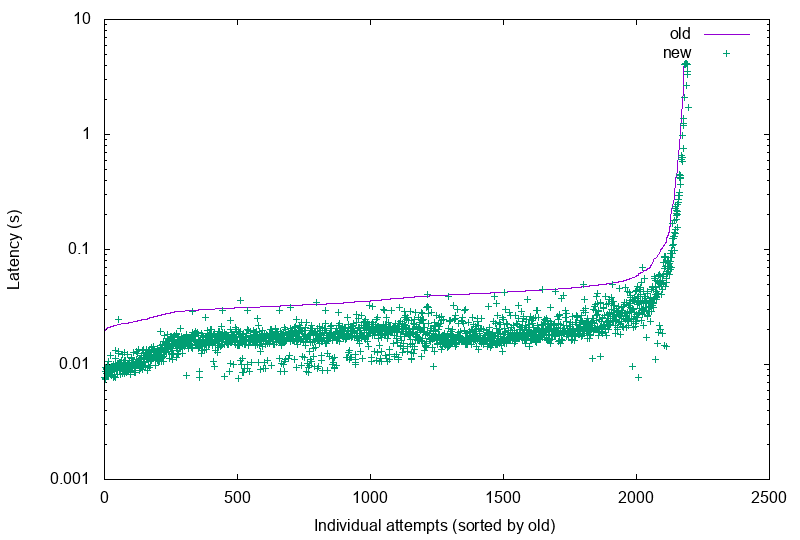
The final result

The final result is rather pleasant (old here is baseline Ruby, new is the new new thing):

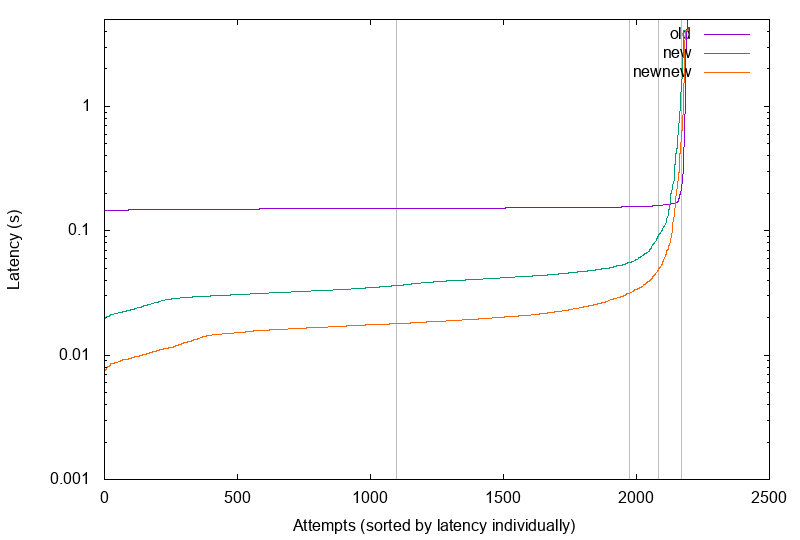
The sheer awesomeness of that result is somewhat lost in the log graph, so let me present one more graph to compare (old = C, new = old Ruby, newnew = new Ruby):

And while it doesn’t beat the C version on the long tail, it’s still a significant improvement on the status quo.

Because not only is the runtime shorter, but for some inputs it manages to find much more anagrams before the 4s self-imposed deadline:

# Three word anagrams with more results
$ awk -F, '$9 > $5 {print $5,$9,$4,$8,NR}' final-raw.csv | sed 's/ /\t/g'
401     1001    4.107699858     3.540053178     50
59      166     4.101503023     4.101624591     762
292     810     4.101906637     4.103267032     814
97      674     4.101492565     4.102817641     850
294     514     4.102067254     4.102588721     1177
60      127     4.10140732      4.101520593     1350
662     1001    4.102990528     2.648105656     1767
50      79      4.104906447     4.101455719     1840
219     1001    4.106455044     3.329974976     1844
172     199     4.101747681     4.101612991     1872
937     1001    4.168557741     1.70192324      2000
5       66      4.10162053      4.101386407     2029
6       46      4.107682562     4.101275427     2157

What changed?

There are five significant changes that led to the result above. I’ll describe them in detail, one after the other.

Different storage / algorithm for weights

If you look back to the previous post, I was describing the storage of “weights” (letter counts) for the words.

Originally I was using a “vector” of weights (in reality a bitshifted (Big)Integer.

So for input great gatsby in my post I said (for simplicity):

g = ('a'..'z').map { |x| "great gatsby".chars.index(x) ? 1 : 0 }
# => [1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0]

but in reality:

g.inject(0) { |m,x| (m<<6) | x }
# => 1449548522995851421868576864080203282890358848

That makes the subtraction dead simple (you’re subtracting two big integers), the overflow detection also easy (you bitwise-and with a bitmask and test for zero).

Where it breaks down (becomes expensive) is when you need to boil the “weights” back down to an “indicator”⁸. Because just like the inject above, you have to mask and bitshift the “weights” 26x to obtain an indicator, which is deadly to performance.

So I opted for the way cool kids (gson.c) are doing it – by using what I call parallel arithmetic.

When you have two numbers with bits abcde and fghij, you can store them as abcdefghij (that’s the bigint approach) or you can store them as [af, bg, ch, di, ej].

What’s the advantage?

For 5-bits per letter weight (and 26 letters) you get an array of 5 elements, with 26-bits (32, really) each.

Subtraction is a slightly more complicated bitwise operation over the elements in sequence (and you get carry at the end!).

But the main killer feature is the computation of indicator from weights– now it takes 5 bitwise OR operations.

This is one of the reasons why the C version is so insanely fast (and doesn’t need bigint math).

Unfortunately in Ruby you pay for this luxury (of having an Array with 5 elements) with memory:

ObjectSpace.memsize_of(1 << (6 * 26))   # => 40
ObjectSpace.memsize_of([1, 2, 3, 4, 5]) # => 80

C’est la vie.

Using lower-level constructs

Another big gain was opting for lower-level constructs (while) instead of some higher-level iterators (inject, N.times).

It was surprising to me, but it makes difference in terms of performance.

Use basic data structures instead of class instances

Another surprise – by using Array directly instead of wrapping it in neat ParallelArith class (like I already described) and by doing the same for dictionary entries (Array instead of nice Struct-derivative) I managed to get ~50% boost in speed.

The downside? Much worse readability. Just imagine reading entry.first, entry.last instead of entry.indicator, entry.word (respectively).

For the speed boost (and Marshal-size boost)? Worth it.

Avoid object creation, at great cost

Object creation is your enemy. No, I’m serious.

And while it will further complicate your code, if you can reuse objects during iteration, you will be that much better off.

Before I show you the fugliness that I did (and it was prime-time fugly), here are some GC numbers after the final benchmark, which requested ~4400 anagrams from each of the instances:

# old
GC.stat[:total_allocated_objects] # => 1_266_130_158

# new
GC.stat[:total_allocated_objects] # =>    12_291_636

Did you spot the difference?

You might be asking yourself… how in the hell? Let me play you the song of my desperate people.

You go from this:

def call_ana
  # ...
  self.ana(out, ef_s, e, limits, limits.maxwords, [], hints)
end

def self.ana(out, dict, entry, limits, maxwords, partial=[], hints=nil) 
  nw = ParallelArith.get(WEIGHT_BITSIZE, nil)
  ne = [nw, TEMP_DICTENTRY_WORD]
  # ...
  dict.each do |k, v|
    v.each do |de|
      # ...
      newpartial = partial.dup << de.last
      # and I'm sure you wouldn't dare: newpartial = partial + [de.last]
      # ...
      if ParallelArith.sub2(WEIGHT_BITSIZE, entry.first, de.first, nw)
        newhash = {ni => dni}
        self.ana(out, newhash, ne, limits, maxwords - 1, partial.dup << de.first, hints)
      end
    end
  end
end

to this vomit-inducing beauty:

def call_ana
  # ...

  # precook the "data" so we don't have to allocate that in ana() constantly
  nws = Array.new(limits.maxwords+1) { ParallelArith.get(WEIGHT_BITSIZE, nil) }
  dta = {nes: nws.map { |x| [x, TEMP_DICTENTRY_WORD] }, nws: nws}
  
  self.ana(out, dta, ef_s, e, limits, limits.maxwords, [], hints)
end

def self.ana(out, dta, dict, entry, limits, maxwords, partial=[], hints=nil) 
  nw = dta[:nws][maxwords]
  ne = dta[:nes][maxwords]
  newpartial = nil
  newhash = nil
  # ...
  dict.each do |k, v|
    v.each do |de|
      # ...
      newpartial = partial.dup << nil if newpartial.nil? # lazy init
      newpartial[-1] = de.last
      # and `newpartial` is as good as newly allocated
      # ...
      if ParallelArith.sub2(WEIGHT_BITSIZE, entry.first, de.first, nw)
        # ... and we didn't have to allocate `nw`
        newhash = {} if newhash.nil? # lazy init
        newhash.clear[ni] = dni
        self.ana(out, dta, newhash, ne, limits, maxwords - 1, newpartial, hints)
        # ^^ and we avoided newhash, newpartial allocation
      end
    end
  end
end

If you’re not feeling at least a little bit iffy about the monstrosity above, I’m doing something wrong with my description of it.

But again, look at the object allocation numbers… and tell me it isn’t worth it (sometimes).

Do not use for loop

This one hit me like a ton of bricks. I’m rather fond of⁹:

for k, v in dict
  # ...
end

which I thought is the exact equivalent of:

dict.each do |k, v|
  # ...
end

Turns out, I’m dead wrong.

The latter is significantly faster, and avoids some unnecessary object creation, too.

Why? Beats me. And I’m too lazy to check the source.

But for performance critical code… for loop is out.

Conclusion

There you have it. I didn’t quite hit the mark with the tail latency, but I did achieve significant boost while staying within the required memory footprint¹⁰.

On the input I was benchmarking against when developing¹¹ I was able to reduce the latency from 4 seconds to 1.7, all the while getting the upper limit of 1000 outputs instead of the paltry 936.

I think I’m Anagrammed out for next few months.

Now I just need to put this to production, and pray that the Heroku worker holds steady.

Because the memory usage did go up somewhat, despite all my tweaks (using jemalloc 3.6.0 and ruby 2.6.5, btw):

# showing RSS, cpu time, process
$ ps axuww | awk '/puma/{print $6, $10, $11, $12, $13, $14, $15, $16}'
164940 0:01 puma 4.3.3 (tcp://0.0.0.0:3000) [heroku]
206688 1:56 puma: cluster worker 0: 27583 [heroku]
206752 2:24 puma: cluster worker 1: 27583 [heroku]
186660 0:01 puma 4.3.3 (tcp://0.0.0.0:3001) [_bench]
229944 1:12 puma: cluster worker 0: 27758 [_bench]
251032 1:16 puma: cluster worker 1: 27758 [_bench]

At this point: Wish me luck?