Engineering a better Anagrammer, part I

Introduction

This post was spurred by my recent chat with a friend of mine on the topic of long term projects.

I told him a tale of how I came to be involved with Anagrammer.org and how it evolved over the decades.

I’m hoping to capture an essence of that multi-decade endeavor¹ while hoping it’s not terribly boring.

Anagrammer?

Anagram – courtesy of Wikipedia’s entry:

An anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once. For example, the word anagram itself can be rearranged into nag a ram, also the word binary into brainy and the word adobe into abode.

Anagram solver (anagrammer) is a computer program generating “all” possible anagrams given some dictionary of words and a user-specified input.

Onwards.

Background

Long ago – in what feels like a past life – I got accidentally pulled into debugging an overload of a PHP shared hosting node. Turns out, one of the multitude of projects running on that hosting was overloading both the database and the PHP frontend.

This was back in the times when running a shared PHP webhosting on a single beefy node was all the rage. It didn’t help that tenant isolation in LAMP stacks was almost non-existent².

I identified the suspect relatively easily (too many hanging db connections and incoming requests) as an anagrammer service. I poked around the website’s codebase (boy, would that land one in a pot of hot water these days), and found it terrible from an algorithm complexity standpoint.

And being the young and naïve asshat I was, I couldn’t help but write a pseudonymous entry on the web’s guestbook page – without any contact info – complaining about the poor algo and its complexity. Indirectly claiming that a half-brained monkey with a wrench could do better.

To my surprise – not even 5 minutes later – the website’s owner³ contacted me on my university email. First asking to confirm if he found the right Wejn, then nudging me whether I could help.

I was floored by his detective skills and agreed to give it a shot.

I helped to fix the most egregious problems with the algorithm and the database setup. The end result was noticeably better but not perfect. And fortunately for me, that codebase seems to be lost to time.

In the meantime we became friends… chatting over email.

Not even a year later, Michal brought to my attention a 1992 entry to the International Obfuscated C Code Contest. More precisely, the winner of “most humorous output” award that year:

/* © Andreas Gustafsson, https://www.ioccc.org/years.html#1992 */
#include <stdio.h> 

long a
[4],b[
4],c[4]
,d[0400],e=1;
typedef struct f{long g
,h,i[4]    ,j;struct f*k;}f;f g,*
l[4096               ]; char h[256],*m,k=3;
                     long n     (o, p,q)long*o,*p,*q;{
                     long r               =4,s,i=0;for(;r--;s=i^
                     *o^*p,                         i=i&*p|(i|*p)&~*o++,*q
                     ++=s,p                         ++);return i;}t(i,p)long*p
                     ;{*c=d               [i],n(a,c,b),n(p,b,p);}u(j)f*j;{j->h
                     =(j->g     =j->i[0]|j->i[1]|j->i[2]|j->i[3])&4095;}v(
j,s)f*               j; {int i; for(j->k->k&&v(j->k, ' '),fseek(
stdin,     j->j, 0);i=getchar(),putchar(i-'\n'?i:s),i-
'\n';);}w(o,r,j,x,p)f*o,*j;long p;{f q;int 
s,i=o->h;q.k=o;r>i?j=l[r=i]:r<i&&
(s=r&~i)?(s|=s>>1, s|=s
>>2,s|=s>>4,s
|=s>>8
,j=l[r
=((r&i
                         |s)&~(s>>1))-1&i]):0;--x;for
                 (;x&&!(p&i);p>>=1);for(;!x&&j;n(o->i,j->i,q.
            i),u(&q),q.g||(q.j=j->j,v(&q,'\n')),j=j->k);for(;x;j=x
         ?j->k:0){for(;!j&&((r=(r&i)-1&i)-i&&(r&p)?2:(x=0));j=l[r]);!
      x||(j->g&~o->g)||n                              (o->i,j->i,q.i)||(
    u(&q), q.j=j                                              ->j,q.g?w(&q
   ,r,j->k,x                                                      ,p):v(&q,
  '\n'));                                                            }}y(){f
 j;char                                                                *z,*p;
for(;m                                                                  ? j.j=
ftell(                                                                  stdin)
,7,(m=                       gets(m                                     ))||w(
&g,315                       *13,l[                                     4095]
 ,k,64*                      64)&0:                                    0;n(g
  .i,j.i,                    b)||(u                                 (&j),j.
   k=l[j.h],l[j.h]= &j,y())){for(z=                             p=h;*z&&(
    d[*z++]||(p=0)););for(z=p?n(j.i                       ,j.i,j.i)+h:"";
  *z;t(*z++,j.i));}}main(o,p)char**              p; {for(;m = *++p;)for(;*m-
'-'?*m:(k= -atoi(m))&0;d[*m]||(d[*m              ]=e,e<<=1),t(*m++,g.i)); u(&
                             g),m=h
                             ,y();}

According to my email archive, that anagramming bad boy is twice as fast as whatever I could come up with at the time.

And to be honest, over the years I’ve spent plenty of time poking around innards of this clever little algorithm, figuring out what makes it tick. And I’m still foggy on some aspects.

Of course, not understanding it fully didn’t stop me from hacking up a trivial mod to run it ~safely with arbitrary user input from PHP:

--- /home/wejn/download/gson.c  2021-09-19 17:40:54.961285046 +0200
+++ /home/wejn/presmycky.c  2021-09-19 17:53:23.402264365 +0200
@@ -1 +1,16 @@
-#include <stdio.h> 
+#include <stdio.h>
+#include <string.h>
+#include <ctype.h>
+
+char P[010000]="./";
+
+
+
+FILE*dctnr;int _etchar(void){return
+getc(dctnr);}_ef(void){return !feof
+(dctnr);}char*_ets(char*m){char *t,
+*r;r=fgets(m,0xff,dctnr);t=strchr(m
+,'\n');if(t){*t=0;}else{while(_ef()
+&&(_etchar()-'\n')||00);}return r;}
+
+
@@ -17 +32 @@
-stdin,    j->j, 0);i=getchar(),putchar(i-'\n'?i:s),i-
+dctnr,    j->j, 0);i=_etchar(),putchar(i-'\n'?i:s),i-
@@ -35,2 +50,2 @@
-ftell(                                 stdin)
-,7,(m=              gets(m                 ))||w(
+ftell(                                 dctnr)
+,7,(m=              _ets(m                 ))||w(
@@ -42 +57 @@
-  *z;t(*z++,j.i));}}main(o,p)char**         p; {for(;m = *++p;)for(;*m-
+  *z;t(*z++,j.i));}}__ep(o,p)char**         p; {for(;m = *++p;)for(;*m-
@@ -45,0 +61,16 @@
+
+
+
+E(w){printf("ERROR:%d\n",w);exit(1)
+;}main(int o,char**p){static int z[
+032],i,u;char**t,*t2;if(o<3)E(1);k=
+atoi(*++p);++p;if(strstr(*p,"..")||
+strchr(*p,'/')||strlen(*p)+strlen(P
+)+1>(sizeof(P)/sizeof(char)))E(02);
+strcat(P,*p);if(!(dctnr=fopen(P,"r"
+)))E(03);for(t=p+001;*t;t++){t2=*t;
+while(*t2){if(isalpha(*t2)){isupper
+(*t2)?*t2=tolower(*t2):0;z[*t2-'a']
+++;}t2++;}}for(i=0;i<26;i++){if(z[i
+]>15)E(4);if(z[i]>0)u=1;}if(!u)E(5)
+;printf("OK\n");return __ep(00,p);}

And while I feel a certain nostalgia towards that solution, I have to admit it’s not all roses.

On certain adversarial inputs it can hang for a good long while (indefinitely?), it requires nontrivial tweaks to the runtime environment to run reasonably⁴, and in this day and age… running an arbitrary binary on a cheap shared hosting isn’t feasible anymore.

Thus, the meat of this post —

Engineering a better solution

In this section I’ll discuss the engineering process of the new solution and a few dead ends I visited during implementation.

Requirements

Any new solution should be again reasonably fast on the dictionaries supplied:

$ wc -l *
 380285 czech.txt
 237918 english.txt
  53790 slovak.txt
 671993 total

It needs to either run fully in PHP⁵, in the browser, or on a free/cheap tier of some of the “PaaS” services. Say, heroku.com, GCP, etc.

It should run maintenance free:

1. It needs to correctly terminate on a fixed timeout.
2. It should be reasonably resistant to basic DoS attempts.

Dead-end 1: emscripten.org

I’ve spent a few hours trying to make a proof of concept work in emscripten⁶.

It’s a fine alternative if you need to run some arbitrary C code in the browser. Unfortunately for this use-case it has two drawbacks:

1. It leaks the dictionaries used, which is unwelcome
2. The code isn’t clean (not that one should expect that from an IOCCC entry), is I/O oriented, and would require non-trivial changes to properly interface with Javascript.

So I gave up on it and moved on.

Dead-end 2: package it as a CGI script on some PaaS

While turning it to a lightweight webserver+cgi docker image would have been a reasonably easy job, I don’t think it satisfies two requirements:

1. It isn’t maintenance free (it requires extensive monitoring to avoid DoS by queries of death (adversary inputs), as mentioned before)
2. It mostly doesn’t fit free/cheap tiers⁷ thanks to CPU burn

Solution - in general

In the end, I opted for developing a Ruby-based version based on some lessons I gleaned from gson.c over the years… and run it on a free tier on Heroku.

The advantage of this approach is the hopefully increased maintainability due to my use of higher-level language. And the fact that Heroku is dead easy to use:

$ grep ^[J#] heroku-config.txt 
JEMALLOC_ENABLED: true
JEMALLOC_VERSION: 3.6.0
# 3.6.0 seems to have lower memory consumption but slightly higher latency
# 5.2.1 has higher memory consumption and slightly better latency
#
# general advice to use jemalloc found via:
# https://www.speedshop.co/2017/12/04/malloc-doubles-ruby-memory.html
# (linked from https://devcenter.heroku.com/articles/ruby-memory-use)
$ ### =--------------------------------------------------------------= ### $
$ grep -v ^= heroku-buildpacks.txt 
1. https://github.com/gaffneyc/heroku-buildpack-jemalloc.git
2. heroku/ruby

The first one is due to:

heroku buildpacks:add --index 1 \
    https://github.com/gaffneyc/heroku-buildpack-jemalloc.git

(via https://github.com/gaffneyc/heroku-buildpack-jemalloc/)
$ ### =--------------------------------------------------------------= ### $
$ cat Procfile 
web: bundle exec puma -C config/puma.rb
$ ### =--------------------------------------------------------------= ### $
$ cat Gemfile
source 'https://rubygems.org'
ruby '>= 2.6.5', '< 2.7'

gem 'puma'
gem 'rack-app'
$ ### =--------------------------------------------------------------= ### $
$ cat config/puma.rb 
workers Integer(ENV['WEB_CONCURRENCY'] || 2)
threads_count = Integer(ENV['MAX_THREADS'] || 5)
threads threads_count, threads_count

preload_app!

rackup      DefaultRackup
port        ENV['PORT']     || 3000
environment ENV['RACK_ENV'] || 'development'
$ ### =--------------------------------------------------------------= ### $
$ wc -l config.ru lib/presmycky.rb 
 108 config.ru
 230 lib/presmycky.rb
 338 total

In the end, it’s a webserver that runs the solver algorithm on each incoming request. Simple.

Solution - algorithm

The trick, of course, is making a fast enough Anagrammer algorithm.

Before you read further, try and think about the task at hand. What would a reasonable algorithm look like?

Here’s my take:

A naïve solution for at most N words is doing a cartesian (cross) join of the dictionary with itself, N times. That becomes highly impractical in a jiffy, given the dictionary is over 380K words.

Not even one cross join is feasible, as the result is north of 144 billion of records.

So there has to be some aggressive trimming going on.

And I’ll trim down the solution to case-insensitive [a-z] inputs, because that makes it much easier, and Czech folks usually don’t mind⁸.

First critical insight – indicator

Having an indicator – a bit vector of all letters of the input alphabet is an extremely powerful trimming factor.

For example, for input great gatsby you end up with:

g = ('a'..'z').map { |x| "great gatsby".chars.index(x) ? 1 : 0 }
# => [1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0]

And when considering a word blame from the dictionary:

b = ('a'..'z').map { |x| "blame".chars.index(x) ? 1 : 0 }
# => [1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

you can simply check if that no letters not present in the input are in the dictionary word:

g.zip(b).map { |x, y| ~x&y }
=> [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

As there are two ones (for l and m), it’s clear that blame isn’t a good word.

And if you generate such an indicator for all of the words in your dictionary, for each unique vector you will end up with a list of candidate words.

Since late, tale, teal, and latte have the same indicator (same letters present).

So not only are you going to end up trimming words that wouldn’t lead anywhere productive, but you also don’t have to traverse the entire dictionary.

On the czech.txt dictionary this leads to 2.66x reduction of entries – 142801 unique indicators out of 380285 unique words. On the english.txt it’s 2.48x.

And better yet, you need one bitwise-and and one is-zero operation per each group of words for the initial trimming. (after all, the indicator fits in 26 bits)

But we can do better.

Second insight – letter counts

By counting the number of individual letters in each word, when we find a matching group by indicator, we can also reject words that have too many individual letters per word.

Poring over the dictionaries, I figured out the “high water mark” for letter frequencies using this script:

#!/usr/bin/ruby

def counts(x)
        x.inject({}) { |m, char| m[char] ||= 0; m[char] += 1; m }
end

require 'pp'
pp File.readlines(ARGV.first || 'data/czech.txt').
        map { |x| x.strip.downcase.scan(/./).sort }.
        inject({}) { |m,x|
                counts(x).each { |k,v| m[k] ||= 0; m[k] = v if v > m[k] }
                m
        }.sort

and the result is surprisingly high – 8 for English (s), 6 for Czech (e, i, o)⁹.

$ ruby highwatermark.rb data/english.txt
[["'", 4],
 ["a", 6],
 ["b", 6],
 ["c", 5],
 ["d", 5],
 ["e", 6],
 ["f", 4],
 ["g", 4],
 ["h", 4],
 ["i", 6],
 ["j", 2],
 ["k", 4],
 ["l", 5],
 ["m", 4],
 ["n", 6],
 ["o", 7],
 ["p", 4],
 ["q", 2],
 ["r", 5],
 ["s", 8],
 ["t", 6],
 ["u", 4],
 ["v", 3],
 ["w", 3],
 ["x", 2],
 ["y", 3],
 ["z", 4]]
$ ruby highwatermark.rb data/czech.txt
[["a", 5],
 ["b", 3],
 ["c", 4],
 ["d", 3],
 ["e", 6],
 ["f", 2],
 ["g", 2],
 ["h", 3],
 ["i", 6],
 ["j", 3],
 ["k", 3],
 ["l", 3],
 ["m", 4],
 ["n", 5],
 ["o", 6],
 ["p", 3],
 ["q", 1],
 ["r", 4],
 ["s", 4],
 ["t", 4],
 ["u", 4],
 ["v", 4],
 ["w", 3],
 ["x", 2],
 ["y", 3],
 ["z", 3]]

But that means that in the worst case (say, max four words per anagram), we need to count to (at most) 32. Inputs with more individual characters doesn’t make sense.

So if we pack the counts for all characters into a single bigint, we can boil this operation down to one bigint subtraction, one bitwise-and, and one is-zero operation. How? By abusing integer overflows:

counts = ->(x) { ('a'..'z').map { |w| x.scan(w).size }.inject(0) { |m,x| m<<4 | x } }
counts['ba'] # => 1346878762742493739090247155712
counts['baa'] # => 2614529362970723140586950361088
counts['ballroom'] # => 1346878762742642393066617438208
# ("%0#{26*4}b" % counts['ballroom']).scan(/..../) => ["0001", "0001", "0000", ...]
mask = 26.times.inject(0) { |m,_| m<<4 | (2**3) } # => 10817285121947557559438534019208
# ('%b' % mask)[0,40] => "1000100010001000100010001000100010001000"
((counts['ballroom'] - counts['baa']) & mask).zero? # => false, oops! baa doesn't fit
((counts['ballroom'] - counts['ba']) & mask).zero? # => true

Third insight – letter counts in remaining dictionary

At this stage, we can expect pretty slimmed down space that we can explore.

For example on the czech dictionary with an “adversary” input dbpezavksjorhylgcutn dbpezavksjorhylgcutn the trimming will cut the full dictionary (380285) to 142801 indexes to search, but then down to 35103 entries based on the indicator but still 89118 unique entries. That is not terrible, but we can still do better.

Another insight we can use – since we’re walking the entire dictionary at least once – is the number of frequencies of individual characters in the words.

Because if we in the first recursion take only the words with the least frequent letter first, we will cut the backtracking significantly.

Relative frequencies for the example above:

[:hints, [
  ["g", 971], ["j", 5365], ["b", 6208], ["d", 9275], ["z", 9710], ["p", 10086],
  ["k", 11191], ["c", 11544], ["h", 12148], ["s", 12513], ["t", 12965],
  ["l", 13385], ["y", 13810], ["v", 13817], ["u", 14855], ["r", 14969],
  ["n", 16046], ["a", 21280], ["o", 21673], ["e", 22054]]]

So instead of recursing for 35103 entries, we only do it for 971 on the first level, and on the next recursion the dictionary will be cut further.

Putting it all together

Thus by aggressively cutting words by character bitmap, further reducing the candidates by letter counts (from the already cut set), and finally recursing first on the least frequent letter, we cut the execution time down significantly.

All of it, of course, comes at a price: memory.

But that is exactly the trade-off I was optimizing for.

As for how significantly? First approximation shows rather promising results:

$ cat oldp
#!/bin/bash
set -e
cd "$(dirname -- "$(readlink -f -- "${0}")" )"/data
ulimit -s 81920
exec ../old/presmycky ${2-3} 1000 czech.txt ${1-michaljirku}
$ ### =-------------------------------------------------------------------= ### $
$ cat newp
#!/bin/bash
cd "$(dirname -- "$(readlink -f -- "${0}")" )"
exec ruby presmycky.rb data/czech.txt ${1-michaljirku} ${2-3} eq 1000
$ ### =-------------------------------------------------------------------= ### $
$ IN=dbpezavksjorhylgcutndbpezavksjorhylgcutn
$ ### =-------------------------------------------------------------------= ### $
$ \time ./oldp $IN 2
OK
0.17user 0.05system 0:00.22elapsed 100%CPU (0avgtext+0avgdata 9772maxresident)k
0inputs+0outputs (0major+2631minor)pagefaults 0swaps
$ ### =-------------------------------------------------------------------= ### $
$ \time ./oldp $IN 3
OK
12.16user 0.05system 0:12.21elapsed 100%CPU (0avgtext+0avgdata 9740maxresident)k
0inputs+0outputs (0major+2636minor)pagefaults 0swaps
$ ### =-------------------------------------------------------------------= ### $
$ \time ./newp $IN 2
dict load took: 0.809s
anagramming took: 0.155s
[]
[:out_size, 0]
anagramming took: 0.155s
0.97user 0.08system 0:01.05elapsed 100%CPU (0avgtext+0avgdata 148760maxresident)k
0inputs+0outputs (0major+38484minor)pagefaults 0swaps
$ ### =-------------------------------------------------------------------= ### $
$ \time ./newp $IN 3
dict load took: 0.803s
anagramming took: 3.534s
[]
[:out_size, 0]
anagramming took: 3.534s
4.37user 0.05system 0:04.42elapsed 100%CPU (0avgtext+0avgdata 148816maxresident)k
0inputs+0outputs (0major+37597minor)pagefaults 0swaps

So, faster on adversarial input for 3-word anagrams at 15.27x more memory. Slower for 2-word anagrams.

It would be nice to have some actual loadtests on actual inputs. Right?

Loadtest

I wrote a basic loadtest, simulating real world use:

#!/usr/bin/env ruby
require 'open-uri'
require 'pp'

Process.setrlimit(Process::RLIMIT_STACK, 81920*1024, 81920*1024)

def old_anagrammer(input, words)
    sz = 0
    a, b = nil
    Dir.chdir('./data') do
        a = Time.now
        w = ["../old/presmycky", words.to_s, 1000.to_s, 'czech.txt', input]
        IO.popen(w, 'r') do |f|
            data = f.read.split(/\n/)
            pp [:old, input, words, data] if $DEBUG
            sz = data.size
        end
        b = Time.now
    end
    [b - a, sz]
end

def new_anagrammer(input, words)
    sz = 0
    a, b = nil
    Dir.chdir('./data') do
        a = Time.now
        u = "http://localhost:3000/anagram?input=#{input}" + 
            "&dict=czech&maxwords=#{words}"
        data = open(u).read.split(/\n/)
        pp [:new, input, words, data] if $DEBUG
        sz = data.size
        b = Time.now
    end
    [b - a, sz]
rescue Net::OpenTimeout
    p [:timeout, input, words]
    retry
end

inputs = File.read('presmy_noaccents').split(/\n/)
for input in inputs
    input_clean = input.chars.reject { |x| x !~ /[a-z]/ }.join
    o2 = old_anagrammer(input_clean, 2)
    o3 = old_anagrammer(input_clean, 3)
    n2 = new_anagrammer(input_clean, 2)
    n3 = new_anagrammer(input_clean, 3)
    puts [input, o2, o3, n2, n3].flatten.map(&:to_s).join(',')
end

and used ~2200 inputs to take it for a spin.

Important to note is that the new anagrammer has built-in hard timeout of 4 seconds. That came in handy on some inputs (e.g. jiri hanzelka a miroslav zikmund) where old anagrammer hung¹⁰ whereas the new one always terminated.

Also, since the new anagrammer runs as a web service that only loads dictionaries on startup, I used HTTP-based interface (running server with $ puma -C config/puma.rb).

I quickly graphed the result:

$ awk -F, '{ print NR,$4,$8,$2,$6 }' < presmy_noaccents.csv > quickplot.data
$ cat <<-'EOF' | gnuplot
set logscale y
set terminal png size 800,540
set output "quickplot.png"
set ylabel "Latency (s)"
set xlabel "Individual attempts"
plot "plot.data" using 1:2 title "old" with points, \
  "plot.data" using 1:3 title "new" with points
exit
EOF

but that tells a mixed story:

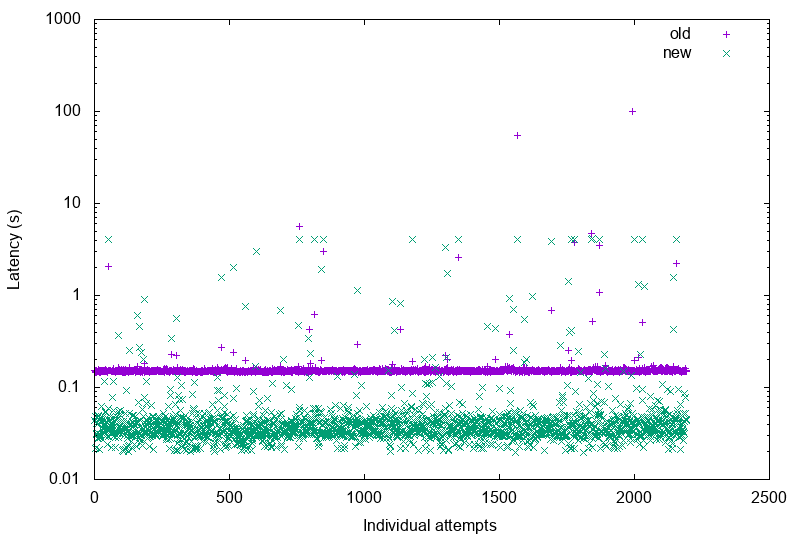
I mean, it clearly hints at the fact that the median latency of the old solution was worse¹¹… but it also hints at some issues with the tail latency of the new solution (there’s more green above the thick purple line).

We need to dig a bit deeper.

One luxury that I normally don’t have at work is that I can directly work with the entire sample set, so drawing percentiles should be easy. None of the sampling/bucketing overkill.

$ ruby -rcsv -e '
all=CSV.new(STDIN).to_a
od2 = all.map { |x| x[1].to_f }.sort
od3 = all.map { |x| x[3].to_f }.sort
nd2 = all.map { |x| x[5].to_f }.sort
nd3 = all.map { |x| x[7].to_f }.sort
puts 1.upto(all.size).to_a.zip(od3).zip(nd3).zip(od2).zip(nd2).
  map { |x| x.flatten.join(" ") }' < presmy_noaccents.csv > sorted.data
$ ENTRIES=$(wc -l <sorted.data)
$ STYLE="nohead lc rgb 'gray'"
$ cat <<-EOF | gnuplot
set ylabel "Latency (s)"
set xlabel "Attempts (sorted by latency individually)"
set logscale y
set terminal png size 800,540
set output "quickplot-sorted.png"
set arrow from $[ $ENTRIES * 50 / 100], graph 0 to $[ $ENTRIES * 50 / 100], graph 1 $STYLE
set arrow from $[ $ENTRIES * 90 / 100], graph 0 to $[ $ENTRIES * 90 / 100], graph 1 $STYLE
set arrow from $[ $ENTRIES * 95 / 100], graph 0 to $[ $ENTRIES * 95 / 100], graph 1 $STYLE
set arrow from $[ $ENTRIES * 99 / 100], graph 0 to $[ $ENTRIES * 99 / 100], graph 1 $STYLE
plot "sorted.data" using 1:2 title "old 3 words" with lines, \\
  "sorted.data" using 1:3 title "new 3 words" with lines, \\
  "sorted.data" using 1:4 title "old 2 words" with points pt 0, \\
  "sorted.data" using 1:5 title "new 2 words" with points pt 0
exit
EOF

And oh boy:

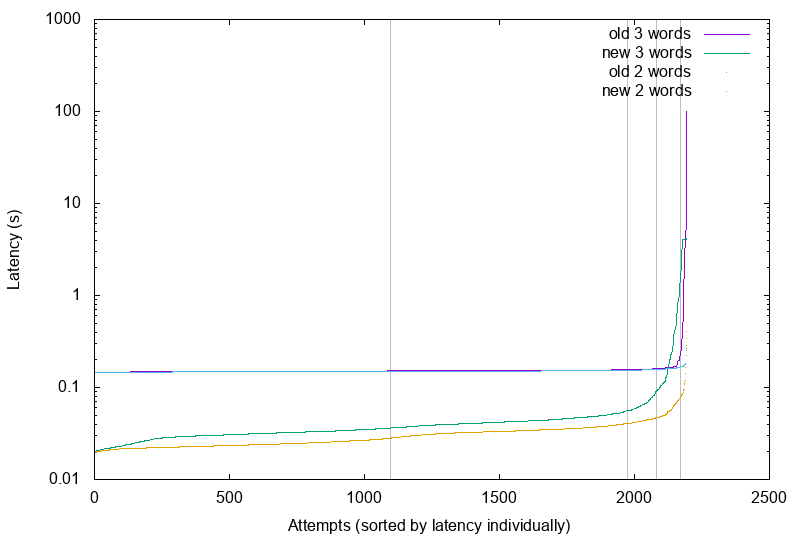click to enlarge; vertical lines mark 50th, 90th, 95th and 99th percentile.

I could basically celebrate that the tail latency isn’t that bad, that it is bounded. And that the median is much better. But I’m somewhat irked by the fact that the new algorithm’s inflection point toward infinity happens much sooner (around 95th percentile instead of 99th).

I’ll have to take a good look at what’s wrong. But that will have to wait until part two of this post, because this one is long enough already.

Closing words

Originally I envisioned this post as a clear cut stroll down the memory lane. Along with some high-level description of the new algorithm.

Alas, my own laziness caught up with me – when I initially implemented the new algo, I neglected to properly loadtest it. Because finding real world data is hard.

Seeing the tail latency now, I feel irked by it. So in the next installment I’ll take a stab at fixing it. No guarantees I’ll be able to. But I’ll at least try.