Overengineering float serialization for no good reason

Problem statement

This is a quick exploration of how overengineering float serialization to be just right(™) instead of needlessly stripping digits off mantissa… wasn’t worth that much.

In other words, say you carefully write 15 lines of python (and some tests) to make 1.234567891e12 and -1.234567891e12 always serialize with max precision to a fixed buffer (say, 14 chars)¹, and avoid this:

a = 1.234567891e12
"%.8g" %  a # => '1.2345679e+12'
"%.8g" % -a # => '-1.2345679e+12'

"%.9g" %  a # => '1.23456789e+12'

# well, shit... what to use, eh?

But… then you think about it for a while… and you realize you were a doofus for not simply phoning it in and just slapping f"{val:.8g}" in there instead.

Why?² Read on…

Background

Before I get to the point, setting up the stage is in order:

I’m slowly wrapping up wavelength calibration support in tobes_ui³ so I can move to the intensity calibration (which I failed to do previously).

During my relaxing times⁴ with the Ocean Optics Flame-S I came across something that seemed like a mistake to me:

import seabreeze.spectrometers as sb
s = sb.Spectrometer.from_first_available()

# Read WLC (Flame-S):
[s.f.eeprom.eeprom_read_slot(i).split(b'\x00')[0] for i in range(1,5)]
# => [b'341.206390', b'0.380489', b'-2.100606e-005', b'-1.107232e-009']

which strangely isn’t present on my Ocean Optics USB4000:

import seabreeze.spectrometers as sb
s = sb.Spectrometer.from_first_available()

# Read WLC (USB4000):
[s.f.eeprom.eeprom_read_slot(i).split(b'\x00')[0] for i in range(1,5)]
# => [b'3.4031543e02', b'2.2877005e-01', b'-1.1263074e-05', b'5.8286309e-10']

Did you spot it? No? Well, the Flame-S has some cali coefficient(s) written as -2.100606e-005, with 3 bytes for exponent, 2 of which unused. ZOMG, the horrors!

That seems like an insane luxury, given that each eeprom slot has 15 bytes, and looks like it’s an ASCII-Z⁵. Which leaves 14 usable bytes for each of the polynomial coefficients. So, using 4-5 of those for exponent (instead of 2-4) seemed like a mistake.

See, the spectrometer returns raw pixel data, and then uses 3rd-degree polynomial (with coefficients stored in eeprom slots 1..4 (X⁰, X¹, X², X³, respectively)) to convert the pixel index to wavelength.

So my natural instinct was to not waste precious bytes of the mantissa and write some beautiful python to minimize waste:

def float_to_string(num, max_len=14):
    """Format float num to string of up to max_len chars, with max precision possible.
 
    The max_len should be at least 8.
    """
    if max_len < 8:
        raise ValueError(f"max_len should be at least 8, is {max_len}")
 
    for precision in range(max_len, 0, -1):
        out = f"{num:.{precision}g}"
        if len(out) <= max_len:
            return out
 
    # Fallback that works (but might be less precise)
    return f"{num:.{max_len-7}e}" if num < 0 else f"{num:.{max_len-6}e}"

But it’s still wasteful, you see:

from tobes_ui.calibration.common import float_to_string
float_to_string(-2.03692509e-09) # => '-2.0369251e-09'

The exponent is -09, not -9. We could still squeeze one moar byte for mantissa.

Should we, though?

This is where I stopped… and investigated.

Solution

As I already mentioned in the Background section, the purpose of the 14-byte representation of each of the 4 floats is to encode the coefficients of a 3rd degree polynomial that is used to convert a pixel index to a wavelength (in nm).

In practical terms, this is a function that goes from 0..2048⁶ to something like 340..1050 (or thereabouts).

So, what does squeezing every single byte for the mantissa actually do?

More Python to find out!

I slopped up⁷ a short script to evaluate the impact of various truncations. For the polynomial I took (newly calibrated) coefficients of my Flame-S that truly has roughly 340..1050 wavelength range⁸:

import numpy as np                                                
import matplotlib.pyplot as plt                                   
                                                                  
original_coeffs = [-2.03692509e-09, -1.83460977e-05, 3.78184170e-01,
                   3.43182843e+02]
 
def poly_eval(coeffs, x):
    return sum(c * x**i for i, c in enumerate(coeffs[::-1]))
 
def truncate_coeffs(coeffs, precision=7):
    out = [float(f"{c:.{precision}e}") for c in coeffs]
 
    print(f"Poly trunc ({precision}):")
    for a, b in zip(coeffs, out):
        print(f"{a} → {b}")
    print()
 
    return out
 
x_vals = np.linspace(0, 2047, 2048)
 
original_values = [poly_eval(original_coeffs, x) for x in x_vals]
 
# Plot it
plt.figure(figsize=(10, 6))
 
max_delta = {}
 
for precision in range(1, 8):
    rounded_coeffs = truncate_coeffs(original_coeffs, precision)
    rounded_values = [poly_eval(rounded_coeffs, x) for x in x_vals]
 
    difference = np.abs(np.array(original_values) - np.array(rounded_values))
    diff = np.max(difference)
    max_delta[precision] = diff
 
    plt.plot(x_vals, difference,
             label=f'{precision} decimal{"" if precision == 1 else "s"}',
             linestyle='-')
 
for precision, diff in max_delta.items():
    print(f"Max Δ ({precision}): {diff} ({diff:.6f})")
 
plt.xlabel('x')
plt.ylabel('|f(x)-f_trunc(x)|')
plt.title('Impact of truncation during float serialization on poly eval')
plt.legend()
#plt.yscale('log')
plt.grid(True)
plt.savefig('trunc.png', dpi=150, bbox_inches='tight')
#plt.show()

Well, the output is curious:

Poly trunc (1):
-2.03692509e-09 → -2e-09
-1.83460977e-05 → -1.8e-05
0.37818417 → 0.38
343.182843 → 340.0
 
Poly trunc (2):
-2.03692509e-09 → -2.04e-09
-1.83460977e-05 → -1.83e-05
0.37818417 → 0.378
343.182843 → 343.0
 
Poly trunc (3):
-2.03692509e-09 → -2.037e-09
-1.83460977e-05 → -1.835e-05
0.37818417 → 0.3782
343.182843 → 343.2
 
Poly trunc (4):
-2.03692509e-09 → -2.0369e-09
-1.83460977e-05 → -1.8346e-05
0.37818417 → 0.37818
343.182843 → 343.18
 
Poly trunc (5):
-2.03692509e-09 → -2.03693e-09
-1.83460977e-05 → -1.83461e-05
0.37818417 → 0.378184
343.182843 → 343.183
 
Poly trunc (6):
-2.03692509e-09 → -2.036925e-09
-1.83460977e-05 → -1.83461e-05
0.37818417 → 0.3781842
343.182843 → 343.1828
 
Poly trunc (7):
-2.03692509e-09 → -2.0369251e-09
-1.83460977e-05 → -1.8346098e-05
0.37818417 → 0.37818417
343.182843 → 343.18284
 
Max Δ (1): 3.182842999999991 (3.182843)
Max Δ (2): 0.3930545959240135 (0.393055)
Max Δ (3): 0.03263497280102001 (0.032635)
Max Δ (4): 0.01075440067290856 (0.010754)
Max Δ (5): 0.0002427423075914703 (0.000243)
Max Δ (6): 4.3000000005122274e-05 (0.000043)
Max Δ (7): 4.342836405157868e-06 (0.000004)

and the graph shows it better:

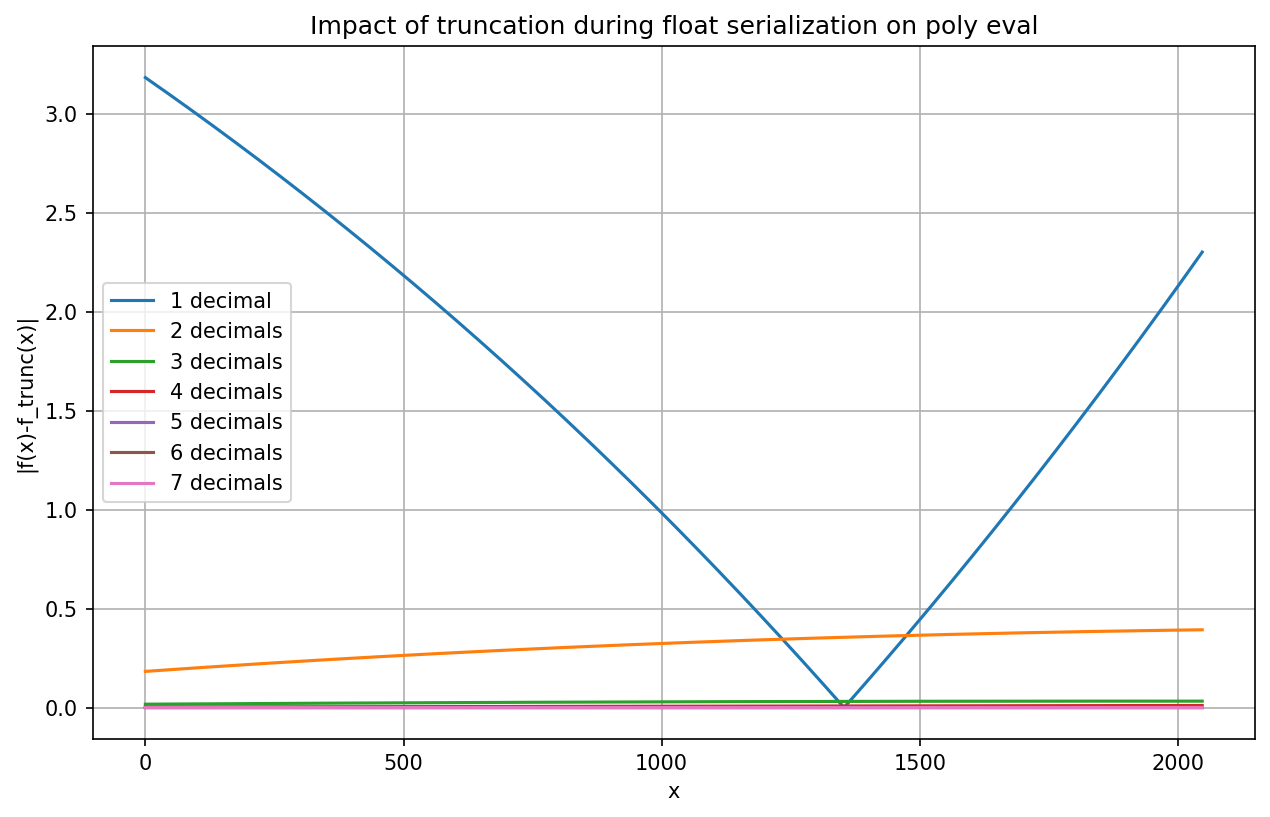
So, yeah, while truncating the mantissa to a single decimal would be a mighty stupid idea (±3.2nm is terrible), the truncation difference from 5th place onward (±0.0002nm or less) is hardly worth talking about, even for high resolution spectrometers⁹.

And the drop of the 8th decimal (resulting in ±0.000004 nm max error) is just a wholly insignificant Δ.

Closing words

I feel a bit silly for wasting a fair bit of time putting that float_to_string commit together¹⁰.

And maybe instead of rushing headlong¹¹ to fix a perceived flaw… a bit more thinking time would be worth it.

Simply said: sometimes, simplicity trumps overengineering.

On the other hand, maybe it makes sense to not stack little flaws… even if I’m not going to add the exponent trimming feature to that func just yet. ;)